《2025年拔尖特训九年级数学上册人教版》

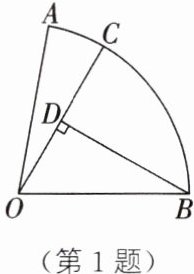
1. (2024·包头)如图,在扇形AOB中,$\angle AOB = 80^\circ$,半径$OA = 3$,C是$\widehat{AB}$上一点,连接OC,D是OC上一点,且$OD = DC$,连接BD.若$BD \perp OC$,则$\widehat{AC}$的长为(B)

A.$\frac{\pi}{6}$
B.$\frac{\pi}{3}$
C.$\frac{\pi}{2}$
D.$\pi$

答案： B

2. (2024·宿迁)如图,正六边形ABCDEF的边长为2,以点E为圆心,EF长为半径画弧,则$\widehat{DF}$的长为 $\underline{\quad\quad}$.

$\frac{4\pi}{3}$

答案： $\frac{4\pi}{3}$

3. (2024·深圳)如图,在矩形ABCD中,$BC = \sqrt{2}AB$,O为BC的中点,$OE = AB = 4$,$\widehat{EF}$与AD相切,则扇形EOF的面积为 $\underline{\quad\quad}$.

4π

答案： $4\pi$

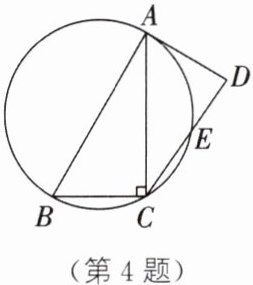
4. 如图,AC为四边形ABCD的对角线,$\angle CAD = 60^\circ$,$\angle ACD = 35^\circ$,$\angle ACB = 90^\circ$,$\triangle ABC$的外接圆交CD于点E,$\widehat{AC}所对圆心角的度数为120^\circ$.
(1) 求证:AD是$\triangle ABC$的外接圆的切线.
(2) 若$\triangle ABC$的外接圆的半径为3,求$\widehat{CE}$的长.

答案：
(1)设圆心为点O，连接OC.
∵∠ACB = 90°，
∴AB是⊙O的直径，即点O在AB上.
∵$\overset{\frown}{AC}$所对圆心角的度数为120°，
∴∠AOC = 120°.
∵OA = OC，
∴∠OAC = ∠OCA = 30°.
∵∠CAD = 60°，
∴∠OAD = ∠OAC + ∠CAD = 90°.
∴OA⊥AD.
∵OA是⊙O的半径，
∴AD是△ABC的外接圆的切线.
(2)连接OE.
∵∠OCA = 30°，∠ACD = 35°，
∴∠OCD = ∠OCA + ∠ACD = 30° + 35° = 65°.
∵OC = OE，
∴∠OEC = ∠OCD = 65°.
∴∠COE = 180° - ∠OCE - ∠OEC = 180° - 65° - 65° = 50°.
∴$\overset{\frown}{CE}$的长 = $\frac{50×\pi×3}{180}=\frac{5\pi}{6}$.

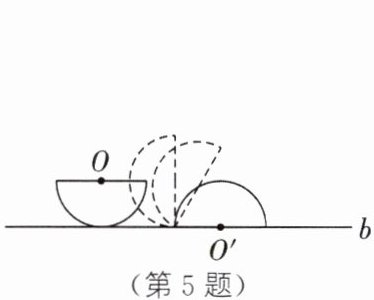
5. 如图,半径为5的半圆的初始状态是直径平行于直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O滚动的路径长为( )


A.$5\pi$
B.$2.5\pi$
C.$5 + 2.5\pi$
D.10

答案：
A 解析:如图，圆心O滚动的路径长 = OE + $\overset{\frown}{EO'}$ = $\frac{1}{4}×2\pi×5+\frac{1}{4}×2\pi×5 = 5\pi$.

6. 如图,正六边形ABCDEF的外接圆$\odot O$的半径为2,过圆心O的两条直线$l_1,l_2的夹角为60^\circ$,则图中的阴影部分的面积为( )


A.$\frac{4}{3}\pi-\sqrt{3}$
B.$\frac{4}{3}\pi-\frac{\sqrt{3}}{2}$
C.$\frac{2}{3}\pi-\sqrt{3}$
D.$\frac{2}{3}\pi-\frac{\sqrt{3}}{2}$

答案：
C 解析:如图，连接AD，OC.
∵⊙O是正六边形的外接圆，
∴AD必过点O，∠COD = $\frac{360^\circ}{6}=60^\circ$.
又
∵OC = OD，
∴△COD是等边三角形，OC = OD = CD = 2.
∴∠OCD = 60°.同理，可得∠OAB = 60°.
∵直线$l_1$，$l_2$的夹角为60°，
∴∠COD - ∠KOD = ∠KOH - ∠KOD，即∠COK = ∠DOH.又
∵∠DOH = ∠AOG，
∴∠COK = ∠AOG.
∵OC = OA，∠OCK = ∠OAG，
∴△OCK≌△OAG.
∵∠COK = ∠AOG，
∴$S_{扇形OCM}=S_{扇形OAN}$.
∴$S_{扇形OCM}-S_{\triangle OCK}=S_{扇形OAN}-S_{\triangle OAG}$.
∴$S_{阴影}=S_{扇形OCD}-S_{\triangle COD}$.
∵$S_{扇形OCD}=\frac{60×\pi×2^2}{360}=\frac{2}{3}\pi$，$S_{\triangle COD}=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$.
∴$S_{阴影}=\frac{2}{3}\pi-\sqrt{3}$.

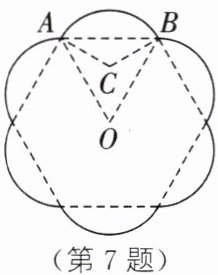
7. (2024·苏州)铁艺花窗是园林设计中常见的装饰元素.如图所示为一个花瓣造型的花窗示意图,该图形由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,$\widehat{AB}$所在圆的圆心C恰好是$\triangle ABO$的内心.若$AB = 2\sqrt{3}$,则该图形的周长(图中实线部分的长度)为 $\underline{\quad\quad}$.

8π

答案： $8\pi$

8. 如图,在$\triangle ABC$中,$\angle BAC = 90^\circ$,$\angle ACB = 30^\circ$,$AB = 2$,将$\triangle ABC$绕直角顶点A按顺时针方向旋转$60^\circ得\triangle ADE$,点C的对应点是E,AC与DE相交于点F,则图中阴影部分的面积为 $\underline{\quad\quad}$.

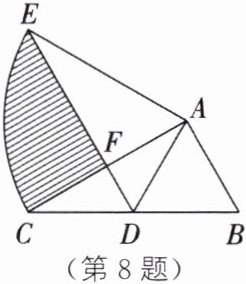
$2\pi-\frac{3\sqrt{3}}{2}$

答案： $2\pi-\frac{3\sqrt{3}}{2}$ 解析:根据题意，可知∠CAE = 60°，△ADE≌△ABC.
∴∠DAE = ∠BAC = 90°，∠AED = ∠ACB = 30°，AD = AB = 2，DE = BC.
∵在Rt△ABC中，∠ACB = 30°，AB = 2，
∴BC = 2AB = 4.
∴AC = $2\sqrt{3}$，DE = 4.
∵∠DAF = ∠EAD - ∠CAE = 90° - 60° = 30°，∠ADF = 90° - 30° = 60°，
∴∠AFD = 90°.
∴DF = $\frac{1}{2}AD = 1$.
∴AF = $\sqrt{3}$.
∴EF = DE - DF = 4 - 1 = 3.
∴$S_{阴影}=S_{扇形ACE}-S_{\triangle AEF}=\frac{60×\pi×(2\sqrt{3})^2}{360}-\frac{1}{2}×\sqrt{3}×3=2\pi-\frac{3\sqrt{3}}{2}$.