《2025年拔尖特训九年级数学上册人教版》

1. ★(2024·湖北)如图,在平面直角坐标系中,点A的坐标为(-4,6),将线段OA绕点O按顺时针方向旋转90°,则点A的对应点A'的坐标为(B)

A.(4,6)
B.(6,4)
C.(-4,-6)
D.(-6,-4)

答案： B

2. 在下列图形中,属于中心对称图形的是(D)

A.
B.
C.
D.

答案： D

3. 如图,在△ABC中,AC= BC,AB= 12,把△ABC绕点A按逆时针方向旋转60°得到△ADE,连接CD.当CD= 2√3时,AC的长为(C)

A.4√3
B.10
C.2√21
D.√21

答案： C

4. 如图,正方形ABCD的边长为4,∠EAF= 45°,将△ABE绕点A按顺时针方向旋转90°得到△ADG.若BE= 1,则DF的长为(C)
A.3
B.√7
C.12/5
D.4

答案： C

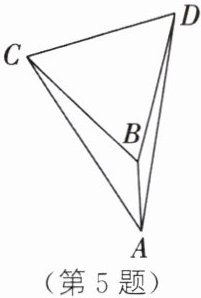
5. 如图,在△ABC中,∠BAC= 30°,AB= 1,AC= 3,以BC为边向右作等边三角形BCD,连接AD,则线段AD的长为______.

答案：
$\sqrt{10}$　解析:如图,将△ABC绕点C按逆时针方向旋转60°得到△EDC,连接AE,则△ACE是等边三角形.
∴∠CEA=60°,∠DEC=∠BAC=30°,DE=BA=1,AE=AC=CE=3.
∴∠AED=∠AEC+∠DEC=60°+30°=90°.在Rt△AED中,AD=$\sqrt{DE²+AE²}$=$\sqrt{1²+3²}$=$\sqrt{10}$
　　　　

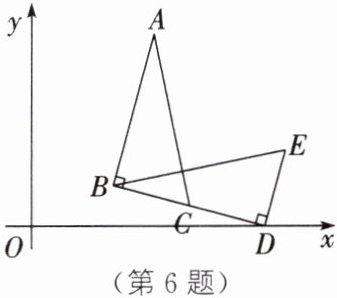
6. 如图,在△BDE中,∠BDE= 90°,BD= 4,点D的坐标是(6,0),∠BDO= 15°,将△BDE旋转到△ABC的位置,C是BD的中点,则旋转中心的坐标为______.

答案：
(6−$\sqrt{2}$,$\sqrt{6}$)　解析:如图,AB与BD的垂直平分线的交点P即为旋转中心，连接PD,过点P作PF⊥x轴于点F.
∵C是BD的中点,
∴易得点P到AB,BD的距离相等，都是$\frac{1}{2}$BD的长，即$\frac{1}{2}$×4=2.
∴易得∠PDB=45°，PD=$\sqrt{2}$×2=2$\sqrt{2}$.
∵∠BDO=15°,
∴∠PDO=45°+15°=60°.
∴∠DPF=30°.
∴DF=$\frac{1}{2}$PD=$\frac{1}{2}$×2$\sqrt{2}$=$\sqrt{2}$.
∵点D的坐标是(6,0),
∴OF=OD−DF=6−$\sqrt{2}$.由勾股定理，得PF=$\sqrt{PD²−DF²}$=$\sqrt{6}$
∴旋转中心的坐标为(6−$\sqrt{2}$,$\sqrt{6}$).

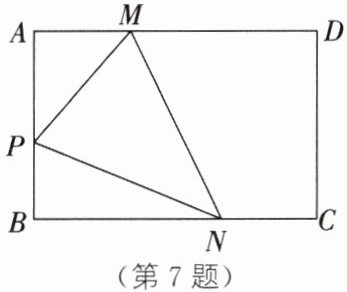
7. 如图,在矩形ABCD中,AB= 4,AD= 6,点P,M,N分别在边AB,AD,BC上运动,且线段MN始终经过矩形的对称中心,则△PMN周长的最小值为______.

答案：
2$\sqrt{13}$+4　解析:如图,点O是矩形的对称中心，取MP的中点Q，连接AQ,OQ,AC,过点O作OG⊥BC,垂足为G,则AQ=PQ=QM=$\frac{1}{2}$PM.
∵线段MN始终经过矩形的对称中心,
∴O是MN的中点.
∴MO=ON=$\frac{1}{2}$MN,OQ=$\frac{1}{2}$PN.易知点O在AC上,且AO=$\frac{1}{2}$AC.
∵AB=4,BC=AD=6,
∴AC=$\sqrt{4²+6²}$=2$\sqrt{13}$.
∴AO=$\sqrt{13}$.
∴C△PMN=PM+PN+MN=2AQ+2OQ+2ON=2(AQ+OQ+ON)≥2(AO+OG)=2($\sqrt{13}$+2)=2$\sqrt{13}$+4.
∴△PMN周长的最小值为2$\sqrt{13}$+4

8. (2024·北京)已知∠MAN= α(0°＜α＜45°),点B,C分别在射线AN,AM上,将线段BC绕点B按顺时针方向旋转180°-2α得到线段BD,过点D作AN的垂线,交射线AM于点E.
(1)如图①,当点D在射线AN上时,求证：C是AE的中点.
(2)如图②,当点D在∠MAN内部时,作DF//AN,交射线AM于点F,试探究线段EF与AC之间的数量关系,并证明.

答案：

(1)如图①,连接CD.
由题意，得BC=BD,∠CBD=180°−2α.
∴∠BDC=∠BCD=$\frac{1}{2}$[180°−(180°−2α)]=α.
∴∠BDC=∠A.
∴CA=CD.
∵DE⊥AN,
∴∠1+∠A=∠2+∠BDC=90°.
∴∠1=∠2.
∴CD=CE.
∴CA=CE.
∴C是AE的中点.
(2)EF=2AC.
如图②,在射线AM上取点H,连接BH,使得BH=BA,取EF的中点G,连接DG,DH.
∵BH=BA,
∴∠A=∠BHA=α.
∴∠ABH=180°−2α=∠CBD.
∴∠ABH−∠CBH=∠CBD−∠CBH,即∠ABC=∠HBD.
又
∵BC=BD,
∴△ABC≌△HBD.
∴AC=HD,∠A=∠BHD=α.
∴∠FHD=∠BHA+∠BHD=2α.
∵DE⊥AN,
∴∠3=90°.
∵DF//AN,
∴∠EFD=∠A=α,∠EDF=∠3=90°.
∵G是EF的中点,
∴GF=GD,EF=2GD.
∴∠GFD=∠GDF=α.
∴∠HGD=2α.
∴∠HGD=∠FHD.
∴DG=DH.
∵AC=HD,
∴DG=AC.
∴EF=2AC.