《2025年拔尖特训九年级数学上册人教版》

9. 如图,在圆内接正六边形 ABCDEF 中,BD,EC 交于点 G.已知半径为$\sqrt{3}$,则 EG 的长为2.

答案： 2　解析:连接BE，GO.
∵六边形ABCDEF为正六边形，
∴BE经过点O，且O是BE的中点，$\angle EDC=\frac{(6 - 2)×180^{\circ}}{6}=120^{\circ}$，$\angle EOG = 90^{\circ}$.
∵DE = DC，
∴$\angle DEC = 30^{\circ}$.
∵BC = CD，
∴$\overset{\frown}{CD}=\overset{\frown}{BC}$.
∴$\angle GEO=\angle DEC = 30^{\circ}$.
∴$OG=\frac{1}{2}EG$.由勾股定理，得$OG^{2}+OE^{2}=EG^{2}$，即$(\frac{1}{2}EG)^{2}+(\sqrt{3})^{2}=EG^{2}$，解得EG = 2(负值舍去).

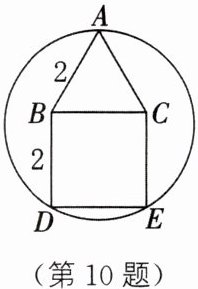
10. 如图,多边形 ABDEC 是由边长为 2 的等边三角形 ABC 和正方形 BDEC 组成的,一圆过 A,D,E 三点,求该圆的半径.

答案：
如图，作AF⊥BC，垂足为F，延长AF交DE于点H.
∵△ABC为等边三角形，
∴AF垂直平分BC，$\angle BAF = 30^{\circ}$.
∵四边形BDEC为正方形，
∴易得AH垂直平分DE.
又
∵DE是圆的弦，
∴AH必过圆心.
记圆心为点O，连接OD，OE.
设$\odot O$的半径为r.
在Rt△ABF中，$\angle BAF = 30^{\circ}$，
∴$BF=\frac{1}{2}AB = 1$.
∴$AF=\sqrt{2^{2}-1^{2}}=\sqrt{3}$.
∴$OH = AF + FH - OA=\sqrt{3}+2 - r$.
在Rt△ODH中，$OH^{2}+DH^{2}=OD^{2}$，即$(2+\sqrt{3}-r)^{2}+1^{2}=r^{2}$，解得$r = 2$.
∴该圆的半径为2.

11. 将三个相同的六角形螺母并排摆放在桌面上,如图①,正六边形的边长为 2 且各有一个顶点在直线 l 上.两侧螺母不动,把中间螺母抽出并重新摆放后,如图②,中间正六边形的两边与直线 l 平行,有两边分别经过两侧正六边形的一个顶点.
(1)∠α＝______.
(2)图②中,中间正六边形的中心到直线 l 的距离为______(结果保留根号).

答案：

(1)30°
(2)$2\sqrt{3}$　解析:如图，记左侧的正六边形在直线l上的顶点为P，中间的正六边形的中心为点O，过点O作ON⊥直线l于点N，交CH于点M，延长AD交直线l于点E，延长CH交GK于点F，延长HC交AD于点B，连接AG.
∵AG//BF，AB//GF，$\angle ABC=\angle GFH = 90^{\circ}$，
∴四边形ABFG是矩形.
∴AB = GF.
∴易得△ABC≌△GFH.
∴BC = FH.
∵PD = 2，
∴易得DE = 1，$PE=\sqrt{3}$.
∴$BF = 2\sqrt{3}$.由正六边形，得$OM=\frac{1}{2}×2\sqrt{3}=\sqrt{3}$.
∵$BC=\frac{1}{2}(BF - CH)=\sqrt{3}-1$，$\angle\alpha = 30^{\circ}$，
∴易得$AB = 3-\sqrt{3}$.
∴$ON = OM + MN = OM + BE = OM + AD + DE - AB=\sqrt{3}+2+1-(3-\sqrt{3})=2\sqrt{3}$.

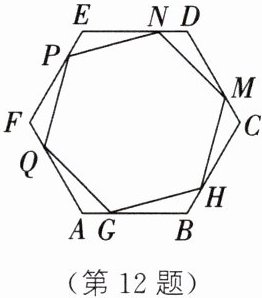
12. 如图所示的正六边形 ABCDEF 是一个创意花坛,AB＝20 m.点 G,H,M,N,P,Q 分别在该正六边形的六条边上,且 AG＝BH＝CM＝DN＝EP＝FQ,现计划在六边形 GHMNPQ 内种植花卉,在剩余部分的六个全等三角形内种植草皮.
(1)正六边形 ABCDEF 的面积是$______m^2. $
(2)当 AG 的长为多少时,草皮的种植面积最大？最大面积是多少？

答案：

(1)$600\sqrt{3}$.
(2)如图，过点G作GS⊥AF，交FA的延长线于点S.
∵$\angle GAS=\frac{360^{\circ}}{6}=60^{\circ}$，
∴$\angle AGS = 30^{\circ}$.
设AG = x m，则$AS=\frac{1}{2}x$ m.
∴$SG=\sqrt{AG^{2}-AS^{2}}=\frac{\sqrt{3}}{2}x$ m.
∵AG = FQ，AB = AF，
∴AQ = BG=(20 - x)m.
设草皮的种植面积为$S\ m^{2}$.
∴易得$S = 6×\frac{1}{2}×(20 - x)×\frac{\sqrt{3}}{2}x=-\frac{3\sqrt{3}}{2}x^{2}+30\sqrt{3}x=-\frac{3\sqrt{3}}{2}(x - 10)^{2}+150\sqrt{3}$.
∵$-\frac{3\sqrt{3}}{2}＜0$，
∴当x = 10时，S的值最大，最大值为$150\sqrt{3}$.
∴当AG = 10 m时，草皮的种植面积最大，最大面积是$150\sqrt{3}\ m^{2}$.