第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 如图,⊙O 是△ABC 的内切圆,D,E 分别为边 AB,AC 上的点,且 DE 为⊙O 的切线. 若△ABC 的周长是 25,BC 的长是 9,则△ADE 的周长是(
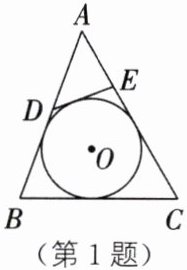
A.7
B.8
C.9
D.16
A
)
A.7
B.8
C.9
D.16
答案:
A
2. 如图,点 O 是△ABC 的内心,∠BAC= 70°,P 为平面内一点,点 O 恰好又是△BCP 的外心,则∠BPC 的度数为(
A.50°
B.55°
C.62.5°
D.65°
C
)A.50°
B.55°
C.62.5°
D.65°
答案:
C
3. 如图,在扇形 ABC 中,CD⊥AB,垂足为 D,⊙E 是△ACD 的内切圆,连接 AE,BE,则∠AEB= ______
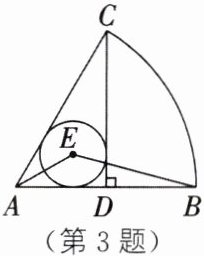
135°
.
答案:
$135^\circ$
4. 如图,边长为 1 的正方形 ABCD 的边 AB 是⊙O 的直径,CF 是⊙O 的切线,E 为切点,点 F 在 AD 上,BE 是⊙O 的弦,求△CDF 的面积.


答案:
设$AF=x$,则$DF=1 - x$。
∵ 四边形ABCD是正方形,
∴ $\angle DAB = \angle CBA = 90^\circ$。
∴ $DA\perp AB$,$CB\perp AB$。
∴ AD是$\odot O$的切线,CB是$\odot O$的切线。
∵ CF是$\odot O$的切线,E为切点,
∴ $EF = AF = x$,$CB = CE = 1$。
∴ $CF = CE + EF = 1 + x$。
∴ 在$Rt\triangle CDF$中,由勾股定理,得$CF^2 = CD^2 + DF^2$,即$(1 + x)^2 = 1 + (1 - x)^2$,解得$x = \frac{1}{4}$。
∴ $DF = 1 - x = \frac{3}{4}$。
∴ $S_{\triangle CDF} = \frac{1}{2}×1×\frac{3}{4} = \frac{3}{8}$。
∵ 四边形ABCD是正方形,
∴ $\angle DAB = \angle CBA = 90^\circ$。
∴ $DA\perp AB$,$CB\perp AB$。
∴ AD是$\odot O$的切线,CB是$\odot O$的切线。
∵ CF是$\odot O$的切线,E为切点,
∴ $EF = AF = x$,$CB = CE = 1$。
∴ $CF = CE + EF = 1 + x$。
∴ 在$Rt\triangle CDF$中,由勾股定理,得$CF^2 = CD^2 + DF^2$,即$(1 + x)^2 = 1 + (1 - x)^2$,解得$x = \frac{1}{4}$。
∴ $DF = 1 - x = \frac{3}{4}$。
∴ $S_{\triangle CDF} = \frac{1}{2}×1×\frac{3}{4} = \frac{3}{8}$。
5. 如图,PA,PB,CD 分别切⊙O 于点 A,B,E,CD 分别交 PA,PB 于点 C,D. 若∠P= 40°,则∠PAE+∠PBE 的度数为(
A.50°
B.62°
C.66°
D.70°
D
)A.50°
B.62°
C.66°
D.70°
答案:
D 解析:
∵ PA,PB,CD分别切$\odot O$于点A,B,E,CD交PA,PB于点C,D,
∴ $CE = CA$,$DE = DB$。
∴ $\angle CAE = \angle CEA$,$\angle DEB = \angle DBE$。
∴ $\angle PCD = \angle CAE + \angle CEA = 2\angle CAE$,$\angle PDC = \angle DEB + \angle DBE = 2\angle DBE$。
∴ $\angle CAE = \frac{1}{2}\angle PCD$,$\angle DBE = \frac{1}{2}\angle PDC$,即$\angle PAE = \frac{1}{2}\angle PCD$,$\angle PBE = \frac{1}{2}\angle PDC$。
∵ $\angle P = 40^\circ$,
∴ $\angle PAE + \angle PBE = \frac{1}{2}\angle PCD + \frac{1}{2}\angle PDC = \frac{1}{2}(\angle PCD + \angle PDC) = \frac{1}{2}(180^\circ - \angle P) = 70^\circ$。
∵ PA,PB,CD分别切$\odot O$于点A,B,E,CD交PA,PB于点C,D,
∴ $CE = CA$,$DE = DB$。
∴ $\angle CAE = \angle CEA$,$\angle DEB = \angle DBE$。
∴ $\angle PCD = \angle CAE + \angle CEA = 2\angle CAE$,$\angle PDC = \angle DEB + \angle DBE = 2\angle DBE$。
∴ $\angle CAE = \frac{1}{2}\angle PCD$,$\angle DBE = \frac{1}{2}\angle PDC$,即$\angle PAE = \frac{1}{2}\angle PCD$,$\angle PBE = \frac{1}{2}\angle PDC$。
∵ $\angle P = 40^\circ$,
∴ $\angle PAE + \angle PBE = \frac{1}{2}\angle PCD + \frac{1}{2}\angle PDC = \frac{1}{2}(\angle PCD + \angle PDC) = \frac{1}{2}(180^\circ - \angle P) = 70^\circ$。
6. 如图,点 I 和 O 分别是△ABC 的内心和外心. 若∠AIB= 125°,则∠AOB 的度数为(
A.120°
B.125°
C.135°
D.140°
D
)A.120°
B.125°
C.135°
D.140°
答案:
D 解析:
∵ 点O是$\triangle ABC$的外心,
∴ $\angle AOB = 2\angle C$。
∴ $\angle C = \frac{1}{2}\angle AOB$。
∵ 点I是$\triangle ABC$的内心,
∴ $\angle IAB = \frac{1}{2}\angle CAB$,$\angle IBA = \frac{1}{2}\angle CBA$。
∴ $\angle AIB = 180^\circ - (\angle IAB + \angle IBA) = 180^\circ - \frac{1}{2}(\angle CAB + \angle CBA) = 180^\circ - \frac{1}{2}(180^\circ - \angle C) = 90^\circ + \frac{1}{2}\angle C$。
∵ $\angle C = \frac{1}{2}\angle AOB$,
∴ $\angle AIB = 90^\circ + \frac{1}{4}\angle AOB$。
∴ $4\angle AIB - \angle AOB = 360^\circ$。
∵ $\angle AIB = 125^\circ$,
∴ $\angle AOB = 140^\circ$。
∵ 点O是$\triangle ABC$的外心,
∴ $\angle AOB = 2\angle C$。
∴ $\angle C = \frac{1}{2}\angle AOB$。
∵ 点I是$\triangle ABC$的内心,
∴ $\angle IAB = \frac{1}{2}\angle CAB$,$\angle IBA = \frac{1}{2}\angle CBA$。
∴ $\angle AIB = 180^\circ - (\angle IAB + \angle IBA) = 180^\circ - \frac{1}{2}(\angle CAB + \angle CBA) = 180^\circ - \frac{1}{2}(180^\circ - \angle C) = 90^\circ + \frac{1}{2}\angle C$。
∵ $\angle C = \frac{1}{2}\angle AOB$,
∴ $\angle AIB = 90^\circ + \frac{1}{4}\angle AOB$。
∴ $4\angle AIB - \angle AOB = 360^\circ$。
∵ $\angle AIB = 125^\circ$,
∴ $\angle AOB = 140^\circ$。
7. 如图,⊙O 的直径 AB= 8,AM,BN 是它的两条切线,DE 与⊙O 相切于点 E,并分别与 AM,BN 相交于 D,C 两点,BD,OC 相交于点 F. 若 CD= 10,则 BF 的长是( )

A.$\frac{8\sqrt{17}}{9}$
B.$\frac{10\sqrt{17}}{9}$
C.$\frac{8\sqrt{15}}{9}$
D.$\frac{10\sqrt{15}}{9}$

A.$\frac{8\sqrt{17}}{9}$
B.$\frac{10\sqrt{17}}{9}$
C.$\frac{8\sqrt{15}}{9}$
D.$\frac{10\sqrt{15}}{9}$
答案:
A 解析:如图,以O为原点建立平面直角坐标系,过点D作$DH\perp BC$于点H。
∵ AB是直径,$AB = 8$,
∴ $OA = OB = 4$。
∵ AD,BC,CD是$\odot O$的切线,
∴ $\angle DAB = \angle ABH = 90^\circ = \angle DHB$,$DA = DE$,$CE = CB$。
∴ 四边形ABHD是矩形。
∴ $AD = BH$,$AB = DH = 8$。
∴ $CH = \sqrt{CD^2 - DH^2} = \sqrt{10^2 - 8^2} = 6$。
设$AD = DE = BH = x$,则$CE = CB = x + 6$。
∴ $x + x + 6 = 10$,解得$x = 2$。
∴ 易得$D(2, 4)$,$C(8, -4)$,$B(0, -4)$。
∴ 易得直线OC对应的函数解析式为$y = -\frac{1}{2}x$,直线BD对应的函数解析式为$y = 4x - 4$。
联立$\begin{cases}y = -\frac{1}{2}x\\y = 4x - 4\end{cases}$,解得$\begin{cases}x = \frac{8}{9}\\y = -\frac{4}{9}\end{cases}$。
∴ $F(\frac{8}{9}, -\frac{4}{9})$。
∴ $BF = \sqrt{(\frac{8}{9})^2 + (-\frac{4}{9} + 4)^2} = \frac{8\sqrt{17}}{9}$。

A 解析:如图,以O为原点建立平面直角坐标系,过点D作$DH\perp BC$于点H。
∵ AB是直径,$AB = 8$,
∴ $OA = OB = 4$。
∵ AD,BC,CD是$\odot O$的切线,
∴ $\angle DAB = \angle ABH = 90^\circ = \angle DHB$,$DA = DE$,$CE = CB$。
∴ 四边形ABHD是矩形。
∴ $AD = BH$,$AB = DH = 8$。
∴ $CH = \sqrt{CD^2 - DH^2} = \sqrt{10^2 - 8^2} = 6$。
设$AD = DE = BH = x$,则$CE = CB = x + 6$。
∴ $x + x + 6 = 10$,解得$x = 2$。
∴ 易得$D(2, 4)$,$C(8, -4)$,$B(0, -4)$。
∴ 易得直线OC对应的函数解析式为$y = -\frac{1}{2}x$,直线BD对应的函数解析式为$y = 4x - 4$。
联立$\begin{cases}y = -\frac{1}{2}x\\y = 4x - 4\end{cases}$,解得$\begin{cases}x = \frac{8}{9}\\y = -\frac{4}{9}\end{cases}$。
∴ $F(\frac{8}{9}, -\frac{4}{9})$。
∴ $BF = \sqrt{(\frac{8}{9})^2 + (-\frac{4}{9} + 4)^2} = \frac{8\sqrt{17}}{9}$。

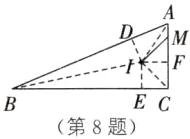
8. *如图,在 Rt△ABC 中,∠C= 90°,AC= 5,BC= 12,AM= 1,点 I 为△ABC 的内心,则 IM= ______.


答案:
$2\sqrt{2}$ 解析:如图,过点I作$ID\perp AB$于点D,$IE\perp BC$于点E,$IF\perp AC$于点F,连接IA,IB,IC。
∵ $\angle ACB = 90^\circ$,$AC = 5$,$BC = 12$,
∴ $AB = \sqrt{AC^2 + BC^2} = \sqrt{5^2 + 12^2} = 13$。
∵ $\angle IEC = \angle IFC = \angle ACB = 90^\circ$,
∴ 四边形IECF是矩形。
∵ 点I为$\triangle ABC$的内心,
∴ $ID = IE = IF$。
∴ 四边形IECF是正方形。
设$CF = IF = ID = IE = r$。
∵ $S_{\triangle AIB} + S_{\triangle BIC} + S_{\triangle AIC} = S_{\triangle ABC}$,
∴ $\frac{1}{2}×13r + \frac{1}{2}×12r + \frac{1}{2}×5r = \frac{1}{2}×12×5$,解得$r = 2$。
∴ $CF = IF = 2$。
∵ $\angle AFI = 90^\circ$,$MF = AC - CF - AM = 5 - 2 - 1 = 2$,
∴ $IM = \sqrt{IF^2 + MF^2} = \sqrt{2^2 + 2^2} = 2\sqrt{2}$。
方法归纳
有关三角形内切圆的两个重要结论
(1) 若三角形的三边长分别为a,b,c,内切圆的半径为r,则三角形的面积$S = \frac{1}{2}(a + b + c)r$。
(2) 若直角三角形的两直角边长分别为a,b,斜边长为c,则此直角三角形内切圆的半径$r = \frac{a + b - c}{2}$或$r = \frac{ab}{a + b + c}$。
$2\sqrt{2}$ 解析:如图,过点I作$ID\perp AB$于点D,$IE\perp BC$于点E,$IF\perp AC$于点F,连接IA,IB,IC。
∵ $\angle ACB = 90^\circ$,$AC = 5$,$BC = 12$,
∴ $AB = \sqrt{AC^2 + BC^2} = \sqrt{5^2 + 12^2} = 13$。
∵ $\angle IEC = \angle IFC = \angle ACB = 90^\circ$,
∴ 四边形IECF是矩形。
∵ 点I为$\triangle ABC$的内心,
∴ $ID = IE = IF$。
∴ 四边形IECF是正方形。
设$CF = IF = ID = IE = r$。
∵ $S_{\triangle AIB} + S_{\triangle BIC} + S_{\triangle AIC} = S_{\triangle ABC}$,
∴ $\frac{1}{2}×13r + \frac{1}{2}×12r + \frac{1}{2}×5r = \frac{1}{2}×12×5$,解得$r = 2$。
∴ $CF = IF = 2$。
∵ $\angle AFI = 90^\circ$,$MF = AC - CF - AM = 5 - 2 - 1 = 2$,
∴ $IM = \sqrt{IF^2 + MF^2} = \sqrt{2^2 + 2^2} = 2\sqrt{2}$。

方法归纳
有关三角形内切圆的两个重要结论
(1) 若三角形的三边长分别为a,b,c,内切圆的半径为r,则三角形的面积$S = \frac{1}{2}(a + b + c)r$。
(2) 若直角三角形的两直角边长分别为a,b,斜边长为c,则此直角三角形内切圆的半径$r = \frac{a + b - c}{2}$或$r = \frac{ab}{a + b + c}$。
9. 如图,△ABC 内接于⊙O,AB 为⊙O 的直径,I 为△ABC 的内心,连接 OI,AI,BI. 若 OI⊥BI,OI= 1,则 AB 的长为
$2\sqrt{5}$
.
答案:
$2\sqrt{5}$ 解析:延长BI交$\odot O$于点M,连接MA。
易知$\angle AMB = \angle ACB = 90^\circ$。
又
∵ $BI\perp OI$,$AO = OB$,
∴ OI为$\triangle AMB$的中位线。
∴ $AM = 2OI = 2$。
在$Rt\triangle ABC$中,I为三个角平分线的交点,
∴ 易得$\angle IAB + \angle IBA = 45^\circ$,即$\angle MIA = 45^\circ$。
∴ $\triangle MAI$为等腰直角三角形。
∴ $MA = MI = IB = 2$。
根据勾股定理,可得$AB^2 = MA^2 + MB^2 = 2^2 + 4^2 = 20$,即$AB = 2\sqrt{5}$。
易知$\angle AMB = \angle ACB = 90^\circ$。
又
∵ $BI\perp OI$,$AO = OB$,
∴ OI为$\triangle AMB$的中位线。
∴ $AM = 2OI = 2$。
在$Rt\triangle ABC$中,I为三个角平分线的交点,
∴ 易得$\angle IAB + \angle IBA = 45^\circ$,即$\angle MIA = 45^\circ$。
∴ $\triangle MAI$为等腰直角三角形。
∴ $MA = MI = IB = 2$。
根据勾股定理,可得$AB^2 = MA^2 + MB^2 = 2^2 + 4^2 = 20$,即$AB = 2\sqrt{5}$。
查看更多完整答案,请扫码查看


