《2025年拔尖特训九年级数学上册人教版》

6. 如图,菱形ABCD的对角线AC,BD相交于点O,P为边AB上一动点(不与点A,B重合),$PE⊥OA$于点E,$PF⊥OB$于点F.若$AB= 8$,$∠BAD= 60°$,设$AP= x$,△OEF的面积是y,则下列图象能大致反映y与x之间的函数关系的是(B)
A.
B.
C.
D.

答案： B

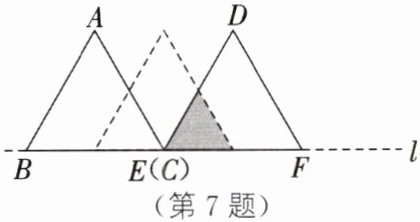
7. 如图,△ABC和△DEF都是边长为2cm的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合,现将△ABC沿着直线l以2cm/s的速度向右移动,△DEF沿着直线l以1cm/s的速度向右移动,直至点B,F重合时停止移动.在此过程中,设点B移动的时间为x s,两个三角形重叠部分的面积为$y cm^2,$则y随x变化的函数图象大致为( )


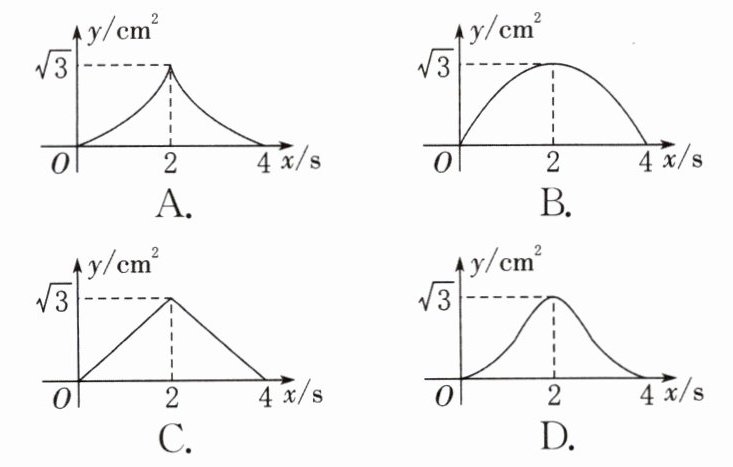
A.
B.
C.
D.

答案：
A 解析：
∵ 将△ABC沿着直线l以2 cm/s的速度向右移动,△DEF沿着直线l以1 cm/s的速度向右移动,
∴ 当点B移动的时间为x s时,△ABC相对于△DEF向右移动了2x-x=x(cm).如图①,当0＜x≤2时,过点G作GH⊥BF于点H.
∵ △ABC和△DEF均为等边三角形,
∴ 易得△GEJ为等边三角形.
∴ EJ=GJ=x cm.
∴ 易得 $ GH=\frac{\sqrt{3}}{2}GJ=\frac{\sqrt{3}}{2}x $ cm.
∴ $ y=\frac{1}{2}\cdot x\cdot \frac{\sqrt{3}}{2}x=\frac{\sqrt{3}}{4}x^{2} $.函数图象的开口向上,且当x=2时,$ y=\sqrt{3} $.如图②,当2＜x≤4时,过点G作GH⊥BF于点H.同理,得△GJF为等边三角形,JF=GF=(4-x)cm.
∴ $ y=\frac{1}{2}(4-x)\cdot \frac{\sqrt{3}}{2}(4-x)=\frac{\sqrt{3}}{4}(4-x)^{2} $,函数图象开口向上.
∴ 选项A符合题意.

8. 二次函数$y= ax^2+bx+c$的部分图象如图所示,则方程$ax^2+bx+c= 0$的所有解的积为(C)
A.-4
B.4
C.-5
D.5

答案： C

9. 如图,抛物线$y= -\frac{1}{2}(x-6)^2+2$与x轴交于点A,B,把抛物线在x轴及其上方的部分记作$C_2$,将$C_2向左平移得到C_1$,$C_1$与x轴交于点O,A.若直线$y= \frac{1}{2}x+m与C_1,C_2$共有3个不同的交点,求m的取值范围.

答案：
∵ 抛物线 $ y=-\frac{1}{2}(x-6)^{2}+2 $ 与x轴交于点A,B,
∴ 易得A(4,0),B(8,0).
∵ 将$ C_{2} $向左平移得到$ C_{1} $,$ C_{1} $与x轴交于点O,A,
∴ 将$ C_{2} $向左平移4个单位长度.
∴ $ C_{1} $所在抛物线对应的函数解析式为$ y=-\frac{1}{2}(x-2)^{2}+2 $.
∵ 当直线$ y=\frac{1}{2}x+m $过点A(4,0)时,与$ C_{1},C_{2} $共有2个交点,
∴ $ 0=\frac{1}{2}× 4+m $,解得m=-2.
∵ 当直线$ y=\frac{1}{2}x+m $与抛物线$ y=-\frac{1}{2}(x-6)^{2}+2 $只有1个交点时,与$ C_{1},C_{2} $共有2个交点,
∴ $ \frac{1}{2}x+m=-\frac{1}{2}(x-6)^{2}+2 $.整理,得$ x^{2}-11x+32+2m=0 $.
∴ $ \Delta=121-4(32+2m)=0 $,解得$ m=-\frac{7}{8} $.
∵ 直线$ y=\frac{1}{2}x+m $与$ C_{1},C_{2} $共有3个不同的交点,
∴ $ -2＜m＜-\frac{7}{8} $.