第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 新考向·数学文化 (2024·深圳)下列用七巧板拼成的图案中,是中心对称图形的为(
A.
B.
C.
D.
C
)A.
B.
C.
D.
答案:
【解析】:
本题考查中心对称图形的定义:
在平面内,把一个图形绕着某个点旋转$180° $,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形。
可以根据中心对称图形的定义,逐项分析如下:
选项A:
图案绕着某个点旋转$180° $后,不能与原来的图形重合,所以不是中心对称图形。
选项B:
图案绕着某个点旋转$180° $后,不能与原来的图形重合,所以不是中心对称图形。
选项C:
图案绕着其中心旋转$180° $后,能与原来的图形重合,所以是中心对称图形。
选项D:
图案绕着某个点旋转$180° $后,不能与原来的图形重合,所以不是中心对称图形。
【答案】:C。
本题考查中心对称图形的定义:
在平面内,把一个图形绕着某个点旋转$180° $,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形。
可以根据中心对称图形的定义,逐项分析如下:
选项A:
图案绕着某个点旋转$180° $后,不能与原来的图形重合,所以不是中心对称图形。
选项B:
图案绕着某个点旋转$180° $后,不能与原来的图形重合,所以不是中心对称图形。
选项C:
图案绕着其中心旋转$180° $后,能与原来的图形重合,所以是中心对称图形。
选项D:
图案绕着某个点旋转$180° $后,不能与原来的图形重合,所以不是中心对称图形。
【答案】:C。
2. (2024·长沙)下列图形中,既是轴对称图形,又是中心对称图形的为(
A.
B.
C.
D.
B
)A.
B.
C.
D.
答案:
【解析】:本题考查轴对称图形和中心对称图形的定义及其判断。
轴对称图形是指图形沿一条直线对折后,两部分能够完全重合;
中心对称图形是指图形绕某一点旋转$180^\circ$后,能够与自身重合。
A选项:正三角形是轴对称图形,但不是中心对称图形,故A错误。
B选项:圆内接正方形既是轴对称图形又是中心对称图形,故B正确。
C选项:五角星是轴对称图形,但不是中心对称图形,故C错误。
D选项:该图形不是轴对称图形,但是中心对称图形,故D错误。
【答案】:B
轴对称图形是指图形沿一条直线对折后,两部分能够完全重合;
中心对称图形是指图形绕某一点旋转$180^\circ$后,能够与自身重合。
A选项:正三角形是轴对称图形,但不是中心对称图形,故A错误。
B选项:圆内接正方形既是轴对称图形又是中心对称图形,故B正确。
C选项:五角星是轴对称图形,但不是中心对称图形,故C错误。
D选项:该图形不是轴对称图形,但是中心对称图形,故D错误。
【答案】:B
3. 有下列图形:①平行四边形;②菱形;③等边三角形;④正方形.其中,既是轴对称图形,又是中心对称图形的为
②④
(填序号).
答案:
【解析】:
题目考查了轴对称图形和中心对称图形的概念。
轴对称图形是指图形关于某条直线(轴)对称,即图形上的每一点关于这条轴都有一个对称点,且这些对称点与原图形上的点一一对应。
中心对称图形是指图形关于某一点(中心)对称,即图形上的每一点关于这个中心都有一个对称点,且这些对称点与原图形上的点一一对应。
接下来,我们逐一分析每个图形:
①平行四边形:只是中心对称图形,不是轴对称图形(特殊的平行四边形如矩形、菱形、正方形除外,但此处指的是一般的平行四边形)。
②菱形:既是轴对称图形(有两条对称轴,分别是两条对角线),又是中心对称图形(中心为两条对角线的交点)。
③等边三角形:是轴对称图形(有三条对称轴,分别是三条中线),但不是中心对称图形。
④正方形:既是轴对称图形(有四条对称轴,分别是两条对角线和两条中垂线),又是中心对称图形(中心为两条对角线的交点)。
因此,既是轴对称图形又是中心对称图形的有②菱形和④正方形。
【答案】:
②④
题目考查了轴对称图形和中心对称图形的概念。
轴对称图形是指图形关于某条直线(轴)对称,即图形上的每一点关于这条轴都有一个对称点,且这些对称点与原图形上的点一一对应。
中心对称图形是指图形关于某一点(中心)对称,即图形上的每一点关于这个中心都有一个对称点,且这些对称点与原图形上的点一一对应。
接下来,我们逐一分析每个图形:
①平行四边形:只是中心对称图形,不是轴对称图形(特殊的平行四边形如矩形、菱形、正方形除外,但此处指的是一般的平行四边形)。
②菱形:既是轴对称图形(有两条对称轴,分别是两条对角线),又是中心对称图形(中心为两条对角线的交点)。
③等边三角形:是轴对称图形(有三条对称轴,分别是三条中线),但不是中心对称图形。
④正方形:既是轴对称图形(有四条对称轴,分别是两条对角线和两条中垂线),又是中心对称图形(中心为两条对角线的交点)。
因此,既是轴对称图形又是中心对称图形的有②菱形和④正方形。
【答案】:
②④
4. 如图①~④所示的图形中,是轴对称图形,但不是中心对称图形的为
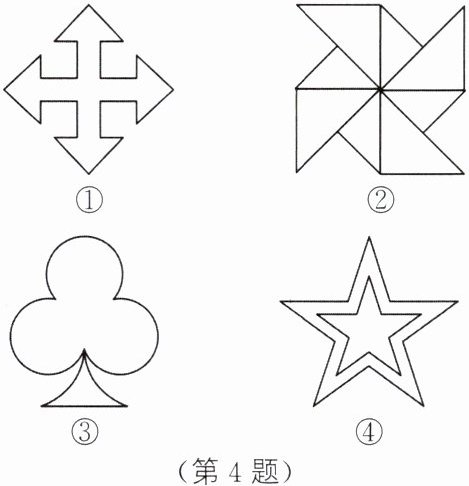
③④
(填序号).
答案:
【解析】:
本题考查轴对称图形和中心对称图形的定义。
轴对称图形是指图形关于某条直线(轴)对称,即图形上的每一点关于这条轴都有对称点。
中心对称图形是指图形关于某一点(中心)对称,即图形上的每一点关于这个中心都有对称点,且这两点到中心的距离相等。
图①既是轴对称图形又是中心对称图形,不符合题意。
图②是中心对称图形,不是轴对称图形,不符合题意。
图③是轴对称图形,不是中心对称图形,符合题意。
图④是轴对称图形,不是中心对称图形,符合题意。
【答案】:③④
本题考查轴对称图形和中心对称图形的定义。
轴对称图形是指图形关于某条直线(轴)对称,即图形上的每一点关于这条轴都有对称点。
中心对称图形是指图形关于某一点(中心)对称,即图形上的每一点关于这个中心都有对称点,且这两点到中心的距离相等。
图①既是轴对称图形又是中心对称图形,不符合题意。
图②是中心对称图形,不是轴对称图形,不符合题意。
图③是轴对称图形,不是中心对称图形,符合题意。
图④是轴对称图形,不是中心对称图形,符合题意。
【答案】:③④
5. 如图,在△ABC中,D是边AB的中点,已知AC= 4,BC= 6.
(1)画出△BDC关于点D的中心对称图形.
(2)根据图形求线段CD长的取值范围.
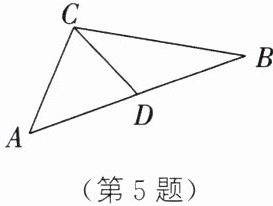
(1)画出△BDC关于点D的中心对称图形.
(2)根据图形求线段CD长的取值范围.

答案:
【解析】:
(1) 根据中心对称的性质,找到点C关于点D的对称点$C^{\prime}$,从而得到$\bigtriangleup BDC$关于点D的中心对称图形$\bigtriangleup ADC^{\prime}$(或描述为将$\bigtriangleup BDC$绕点D旋转$180^{\circ}$得到$\bigtriangleup ADC^{\prime}$)。由于D是AB的中点,所以$AD = BD$,且旋转后$C^{\prime}D = CD$,$AC^{\prime} = BC$。
(2) 在$\bigtriangleup AC^{\prime}C$中,利用三角形的三边关系来求CD的取值范围。已知$AC = 4$,$AC^{\prime} = BC = 6$,根据三角形的三边关系,有:
$AC^{\prime} - AC < CC^{\prime} < AC + AC^{\prime}$,
即:
$6 - 4 < CC^{\prime} < 6 + 4$,
$2 < CC^{\prime} < 10$,
由于D是$CC^{\prime}$的中点,所以:
$1 < CD < 5$。
【答案】:
(1) 图略(按照中心对称的性质画出$\bigtriangleup ADC^{\prime}$即可)。
(2) $1 < CD < 5$。
(1) 根据中心对称的性质,找到点C关于点D的对称点$C^{\prime}$,从而得到$\bigtriangleup BDC$关于点D的中心对称图形$\bigtriangleup ADC^{\prime}$(或描述为将$\bigtriangleup BDC$绕点D旋转$180^{\circ}$得到$\bigtriangleup ADC^{\prime}$)。由于D是AB的中点,所以$AD = BD$,且旋转后$C^{\prime}D = CD$,$AC^{\prime} = BC$。
(2) 在$\bigtriangleup AC^{\prime}C$中,利用三角形的三边关系来求CD的取值范围。已知$AC = 4$,$AC^{\prime} = BC = 6$,根据三角形的三边关系,有:
$AC^{\prime} - AC < CC^{\prime} < AC + AC^{\prime}$,
即:
$6 - 4 < CC^{\prime} < 6 + 4$,
$2 < CC^{\prime} < 10$,
由于D是$CC^{\prime}$的中点,所以:
$1 < CD < 5$。
【答案】:
(1) 图略(按照中心对称的性质画出$\bigtriangleup ADC^{\prime}$即可)。
(2) $1 < CD < 5$。
6. 如图,在四边形ABCD中,AB//CD,AB=CD,对角线AC与BD交于点O,E是AD的中点,连接OE,△ABD的周长为12 cm,则下列结论中,错误的是(
A.OE//AB
B.四边形ABCD是中心对称图形
C.△EOD的周长为3 cm
D.若∠ABC=90°,则四边形ABCD是轴对称图形
C
)A.OE//AB
B.四边形ABCD是中心对称图形
C.△EOD的周长为3 cm
D.若∠ABC=90°,则四边形ABCD是轴对称图形
答案:
【解析】:本题可根据平行四边形的判定与性质、中心对称图形和轴对称图形的定义来逐一分析选项。
选项A:判断OE//AB是否成立
已知在四边形ABCD中,AB//CD,AB = CD,根据一组对边平行且相等的四边形是平行四边形,可得四边形ABCD是平行四边形。
因为平行四边形的对角线互相平分,所以O是BD的中点,又因为E是AD的中点,根据三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,在$\triangle ABD$中,OE是中位线,所以OE//AB,该选项正确。
选项B:判断四边形ABCD是中心对称图形是否成立
由于四边形ABCD是平行四边形,而平行四边形是中心对称图形,对称中心是两条对角线的交点,所以四边形ABCD是中心对称图形,该选项正确。
选项C:判断$\triangle EOD$的周长为3cm是否成立
已知$\triangle ABD$的周长为$12cm$,即$AB + AD + BD = 12cm$。
因为四边形ABCD是平行四边形,所以$AB = CD$,$AD = BC$,$BD = AC$(平行四边形对边相等,对角线互相平分),且$OD=\frac{1}{2}BD$,$DE=\frac{1}{2}AD$,$OE=\frac{1}{2}AB$。
$\triangle EOD$的周长为$OD + DE + OE=\frac{1}{2}(BD + AD + AB)=\frac{1}{2}×12 = 6cm\neq3cm$,该选项错误。
选项D:判断若$\angle ABC = 90^{\circ}$,则四边形ABCD是轴对称图形是否成立
若$\angle ABC = 90^{\circ}$,因为四边形ABCD是平行四边形,有一个角是直角的平行四边形是矩形,所以四边形ABCD是矩形。
矩形是轴对称图形,有两条对称轴,所以若$\angle ABC = 90^{\circ}$,则四边形ABCD是轴对称图形,该选项正确。
综上,答案选C。
【答案】:C
选项A:判断OE//AB是否成立
已知在四边形ABCD中,AB//CD,AB = CD,根据一组对边平行且相等的四边形是平行四边形,可得四边形ABCD是平行四边形。
因为平行四边形的对角线互相平分,所以O是BD的中点,又因为E是AD的中点,根据三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,在$\triangle ABD$中,OE是中位线,所以OE//AB,该选项正确。
选项B:判断四边形ABCD是中心对称图形是否成立
由于四边形ABCD是平行四边形,而平行四边形是中心对称图形,对称中心是两条对角线的交点,所以四边形ABCD是中心对称图形,该选项正确。
选项C:判断$\triangle EOD$的周长为3cm是否成立
已知$\triangle ABD$的周长为$12cm$,即$AB + AD + BD = 12cm$。
因为四边形ABCD是平行四边形,所以$AB = CD$,$AD = BC$,$BD = AC$(平行四边形对边相等,对角线互相平分),且$OD=\frac{1}{2}BD$,$DE=\frac{1}{2}AD$,$OE=\frac{1}{2}AB$。
$\triangle EOD$的周长为$OD + DE + OE=\frac{1}{2}(BD + AD + AB)=\frac{1}{2}×12 = 6cm\neq3cm$,该选项错误。
选项D:判断若$\angle ABC = 90^{\circ}$,则四边形ABCD是轴对称图形是否成立
若$\angle ABC = 90^{\circ}$,因为四边形ABCD是平行四边形,有一个角是直角的平行四边形是矩形,所以四边形ABCD是矩形。
矩形是轴对称图形,有两条对称轴,所以若$\angle ABC = 90^{\circ}$,则四边形ABCD是轴对称图形,该选项正确。
综上,答案选C。
【答案】:C
7. 如图,在菱形ABCD中,AB= 2,∠A= 120°,过菱形ABCD的对称中心O作EG⊥AB于点E,交CD于点G,作FH⊥BC于点F,交AD于点H,则四边形EFGH的周长为(
A.$3+\sqrt{3}$
B.$2+2\sqrt{3}$
C.$2+\sqrt{3}$
D.$1+\sqrt{3}$
B
)A.$3+\sqrt{3}$
B.$2+2\sqrt{3}$
C.$2+\sqrt{3}$
D.$1+\sqrt{3}$
答案:
【解析】:本题可先根据菱形的性质求出相关角度和线段长度,再利用直角三角形的性质求出四边形$EFGH$各边的长度,进而求出其周长。
步骤一:分析菱形的性质
已知四边形$ABCD$是菱形,$\angle A = 120^{\circ}$,根据菱形的性质:菱形的邻角互补,可得$\angle B = 180^{\circ} - 120^{\circ} = 60^{\circ}$;菱形的对角线互相垂直且平分,$O$是菱形$ABCD$的对称中心,即$O$是$AC$、$BD$的交点,所以$AC\perp BD$,$AO = OC$,$BO = OD$,$AB = BC = CD = DA = 2$。
步骤二:求出$\angle ABO$和$\angle BAO$的度数
因为$AC\perp BD$,$\angle A = 120^{\circ}$,$AB = AD$,所以$\triangle ABD$是等腰三角形,根据等腰三角形三线合一的性质,$AC$平分$\angle BAD$,则$\angle BAO = \frac{1}{2}\angle BAD = \frac{1}{2}×120^{\circ} = 60^{\circ}$,那么$\angle ABO = 90^{\circ} - 60^{\circ} = 30^{\circ}$。
步骤三:求出$AO$、$BO$的长度
在$Rt\triangle ABO$中,$\angle ABO = 30^{\circ}$,$AB = 2$,根据$30^{\circ}$所对的直角边等于斜边的一半,可得$AO = \frac{1}{2}AB = 1$,再根据勾股定理$BO = \sqrt{AB^{2} - AO^{2}} = \sqrt{2^{2} - 1^{2}} = \sqrt{3}$。
步骤四:求出$OE$、$OF$的长度
因为$EG\perp AB$,$FH\perp BC$,$O$是菱形$ABCD$的对称中心,所以$OE = OF$,且$OE$是$Rt\triangle ABO$斜边$AB$上的高。
根据三角形面积公式$S = \frac{1}{2}×底×高$,可得$S_{\triangle ABO} = \frac{1}{2}AB\cdot OE = \frac{1}{2}AO\cdot BO$,即$\frac{1}{2}×2×OE = \frac{1}{2}×1×\sqrt{3}$,解得$OE = \frac{\sqrt{3}}{2}$,所以$OF = \frac{\sqrt{3}}{2}$。
步骤五:求出$EH$、$EF$的长度
因为$EG\perp AB$,$FH\perp BC$,$AD// BC$,$AB// CD$,所以四边形$EFGH$是矩形,则$EH = FG$,$EF = HG$。
又因为$O$是$EG$、$FH$的中点,所以$EH = 2OE = \sqrt{3}$,$EF = 2OF\cos30^{\circ}=2×\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2} = 1$(这里$OF$与$BC$夹角为$30^{\circ}$,$EF$为$OF$在水平方向的投影的$2$倍 )。
步骤六:计算四边形$EFGH$的周长
四边形$EFGH$的周长为$2(EH + EF) = 2(\sqrt{3} + 1)=2 + 2\sqrt{3}$。
【答案】:B
步骤一:分析菱形的性质
已知四边形$ABCD$是菱形,$\angle A = 120^{\circ}$,根据菱形的性质:菱形的邻角互补,可得$\angle B = 180^{\circ} - 120^{\circ} = 60^{\circ}$;菱形的对角线互相垂直且平分,$O$是菱形$ABCD$的对称中心,即$O$是$AC$、$BD$的交点,所以$AC\perp BD$,$AO = OC$,$BO = OD$,$AB = BC = CD = DA = 2$。
步骤二:求出$\angle ABO$和$\angle BAO$的度数
因为$AC\perp BD$,$\angle A = 120^{\circ}$,$AB = AD$,所以$\triangle ABD$是等腰三角形,根据等腰三角形三线合一的性质,$AC$平分$\angle BAD$,则$\angle BAO = \frac{1}{2}\angle BAD = \frac{1}{2}×120^{\circ} = 60^{\circ}$,那么$\angle ABO = 90^{\circ} - 60^{\circ} = 30^{\circ}$。
步骤三:求出$AO$、$BO$的长度
在$Rt\triangle ABO$中,$\angle ABO = 30^{\circ}$,$AB = 2$,根据$30^{\circ}$所对的直角边等于斜边的一半,可得$AO = \frac{1}{2}AB = 1$,再根据勾股定理$BO = \sqrt{AB^{2} - AO^{2}} = \sqrt{2^{2} - 1^{2}} = \sqrt{3}$。
步骤四:求出$OE$、$OF$的长度
因为$EG\perp AB$,$FH\perp BC$,$O$是菱形$ABCD$的对称中心,所以$OE = OF$,且$OE$是$Rt\triangle ABO$斜边$AB$上的高。
根据三角形面积公式$S = \frac{1}{2}×底×高$,可得$S_{\triangle ABO} = \frac{1}{2}AB\cdot OE = \frac{1}{2}AO\cdot BO$,即$\frac{1}{2}×2×OE = \frac{1}{2}×1×\sqrt{3}$,解得$OE = \frac{\sqrt{3}}{2}$,所以$OF = \frac{\sqrt{3}}{2}$。
步骤五:求出$EH$、$EF$的长度
因为$EG\perp AB$,$FH\perp BC$,$AD// BC$,$AB// CD$,所以四边形$EFGH$是矩形,则$EH = FG$,$EF = HG$。
又因为$O$是$EG$、$FH$的中点,所以$EH = 2OE = \sqrt{3}$,$EF = 2OF\cos30^{\circ}=2×\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2} = 1$(这里$OF$与$BC$夹角为$30^{\circ}$,$EF$为$OF$在水平方向的投影的$2$倍 )。
步骤六:计算四边形$EFGH$的周长
四边形$EFGH$的周长为$2(EH + EF) = 2(\sqrt{3} + 1)=2 + 2\sqrt{3}$。
【答案】:B
查看更多完整答案,请扫码查看


