《2025年拔尖特训九年级数学上册人教版》

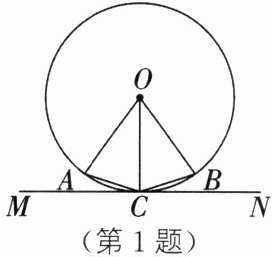
1. (2024·福建)如图,点 A,B 在⊙O 上,∠AOB= 72°,直线 MN 与⊙O 相切,切点为 C,且 C 为$\overset{\frown}{AB}$的中点,则∠ACM 的度数为(A)

A.18°
B.30°
C.36°
D.72°
]

答案： A

2. 如图,在△ABC 中,AB= AC,O 是边 BC 上一点,以点 O 为圆心、OB 长为半径作⊙O,与边 AC 相切于点 A.若 BC= 9,则 OB 的长为3.

答案： 3

3. 如图,AB 是⊙O 的直径,AC,CD 是⊙O 的弦,且 CD⊥AB,垂足为 E,连接 BD,过点 B 作⊙O 的切线,交 AC 的延长线于点 F.
(1)求证：∠ABD= ∠F.
(2)若 E 是 OB 的中点,且 OE= 1,求线段 BF 的长.
]

答案：
(1)
∵BF与⊙O相切于点B，
∴∠ABF=90°.
∴∠A+∠F=90°.
∵CD⊥AB,
∴∠DEB=90°.
∴∠D+∠ABD=90°.
∵∠A=∠D,
∴∠ABD=∠F.
(2)连接OC,BC.
∵AB⊥CD,E是OB的中点,
∴OB=2OE=2,CD是OB的垂直平分线.
∴OC=BC.
∵OC=OB,
∴OC=BC=OB.
∴△OBC是等边三角形.
∴∠COB=60°.
∴∠A=$\frac{1}{2}$∠COB=30°.
∵在Rt△ABF中,AB=2OB=4,
∴易得BF=$\frac{4\sqrt{3}}{3}$.

4. 如图,在平面直角坐标系中,点 P 在第一象限,⊙P 与 x 轴、y 轴都相切,且经过矩形 AOBC 的顶点 C,与 BC 相交于点 D.若⊙P 的半径为 5,点 A 的坐标是(0,8),则点 D 的坐标是((9,2))
A.(9,2)
B.(9,3)
C.(10,2)
D.(10,3)
]

答案： A　解析:如图,设⊙P与x轴、y轴分别相切于点F,E,连接PE,PF,PD,延长EP与CD交于点G,则PE⊥y轴,PF⊥x轴.
∵∠EOF=∠PEO=∠PFO=90°,
∴四边形PEOF为矩形.
∵PE=PF,
∴四边形PEOF为正方形.
∴OE=PF=PE=OF=5,PE//OF.
∵点A的坐标是(0,8),
∴OA=8.
∴AE=8−5=3.
∵四边形AOBC为矩形，
∴BC=OA=8,BC//OA,AC//OB.
∴EG//AC.
∴四边形AEGC为平行四边形，四边形OEGB为平行四边形.
∴CG=AE=3,EG=OB.
∵PE⊥AO,AO//CB,
∴PG⊥CD.
∴CD=2CG=6.
∴DB=BC−CD=8−6=2.
∵PD=5,DG=CG=3,
∴PG=4.
∴OB=EG=5+4=9.
∴点D的坐标是(9,2).

5. 如图,在△ABC 中,AB= BC,AB 为⊙O 的直径,AC 与⊙O 相交于点 D,过点 D 作 DE⊥BC 于点 E,CB 的延长线交⊙O 于点 F.若 BE= 1,BF= 2,则 AD 的长为(C)
A.2
B.3
C.2$\sqrt{3}$
D.$\sqrt{10}$
]

答案： C　解析:连接OF,过点O作OH⊥CF于点H.
∵DE⊥BC,
∴∠EDC+∠C=90°.
∵OA=OD,
∴∠OAD=∠ODA.
∵AB=BC,
∴∠BAC=∠C.
∴∠ODA=∠C.
∴∠EDC+∠ODA=90°.
∴∠ODE=90°.又
∵OH⊥CF,DE⊥BC,
∴∠OHE=∠DEH=90°.
∴四边形ODEH是矩形.
∴OD=EH,OH=DE.
∵OF=OB,
∴BH=FH=1.
∴OB=OD=EH=2.
∴AB=2OD=4,OH=$\sqrt{OB^2 - BH^2}$=$\sqrt{3}$.
∴DE=OH=$\sqrt{3}$.
∴BD=$\sqrt{DE^2 + BE^2}$=2.
∴AD=$\sqrt{AB^2 - BD^2}$=$\sqrt{4^2 - 2^2}$=2$\sqrt{3}$.

6. 如图,AB,AC 分别是⊙O 的直径和弦,OD⊥AB,交 AC 于点 D.过点 B 作⊙O 的切线,与 AC 的延长线交于点 E,连接 BC.若 CD= OD,CE= 1,则 AB 的长为______2$\sqrt{3}$.

答案： 2$\sqrt{3}$　解析:连接BD.
∵AB是⊙O的直径，
∴∠ACB=90°.
∴BC⊥CD.
∵OD⊥AB,CD=OD,
∴BD平分∠ABC.
∴∠ABD=∠CBD.
∵OA=OB,OD⊥AB,
∴AD=DB.
∴∠A=∠ABD=∠CBD.又
∵易得∠A+∠ABC=90°,
∴∠A+∠ABD+∠CBD=90°.
∴∠A=∠ABD=∠CBD=30°.
∵BE是⊙O的切线,
∴∠ABE=90°.
∴∠CBE=90°−2×30°=30°.
∵易得∠BCE=90°,
∴BE=2CE=2.
∵∠A=30°,
∴AE=4.
∴AB=$\sqrt{4^2 - 2^2}$=2$\sqrt{3}$.

7. 如图,在 Rt△ACB 中,∠C= 90°,∠A= 30°,BC= 2$\sqrt{3}$,BD 平分∠ABC,P 为线段 BD 上一动点.以点 P 为圆心、1 为半径作圆,当⊙P 与△ACB 的边相切时,PB 的长为2或4 - $\frac{2\sqrt{3}}{3}$.

答案： 2或4 - $\frac{2\sqrt{3}}{3}$　解析:
∵∠C=90°,∠A=30°,
∴∠ABC=60°.
∵BD平分∠ABC,
∴∠ABD=∠CBD=30°.
∵BC=2$\sqrt{3}$，
∴易知DC=2,BD=4.①如图①,若⊙P与BC相切于点E,连接PE,则∠PEB=90°.
∵PE=1,∠PBE=30°,
∴PB=2.过点P作PF⊥AB于点F.
∵BD平分∠ABC,
∴PE=PF.
∴此时⊙P与AB相切.②如图②,若⊙P与AC相切于点E,连接PE,则PE⊥AC.
∴PE//BC.
∴∠DPE=∠CBD=30°.
∵PE=1,
∴易得DE=$\frac{\sqrt{3}}{3}$.
∴PD=2DE=$\frac{2\sqrt{3}}{3}$.
∴PB=BD−PD=4−$\frac{2\sqrt{3}}{3}$.综上所述，当⊙P与△ACB的边相切时，PB的长为2或4 - $\frac{2\sqrt{3}}{3}$.

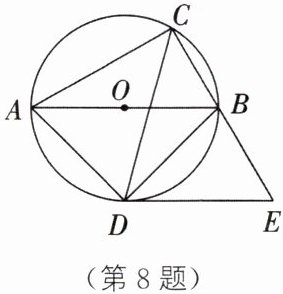
8. *如图,AB 为⊙O 的直径,点 C 在⊙O 上,∠ACB 的平分线 CD 交⊙O 于点 D,过点 D 作 DE//AB,交 CB 的延长线于点 E,连接 AD.
(1)求证：直线 DE 是⊙O 的切线.
(2)若∠BAC= 30°,BC= 2$\sqrt{2}$,求 CD 的长.
]

答案：
(1)连接OD.
∵CD是∠ACB的平分线,
∴∠ACD=∠BCD.
∴∠AOD=∠BOD.
∵AB为⊙O的直径，
∴∠AOD=∠BOD=90°.
∴OD⊥AB.
∵DE//AB,
∴OD⊥DE.
∵OD为⊙O的半径，
∴直线DE是⊙O的切线.
(2)过点B作BF⊥CD于点F.
∵AB为⊙O的直径，
∴∠ACB=90°,∠ADB=90°.
∵∠BAC=30°,BC=2$\sqrt{2}$,
∴AB=2BC=4$\sqrt{2}$.
∵CD是∠ACB的平分线,
∴∠ACD=∠BCD=45°.
∴$\overset{\frown}{AD}$=$\overset{\frown}{BD}$.
∴易知AD=BD=$\frac{\sqrt{2}}{2}$AB=4.
∵∠CDB=∠CAB=30°,
∴BF=$\frac{1}{2}$BD=2.
∴DF=$\sqrt{BD^2 - BF^2}$=2$\sqrt{3}$.
∵BF⊥CD,∠BCD=45°,
∴△BFC为等腰直角三角形.
∴CF=BF=2.
∴CD=CF+DF=2+2$\sqrt{3}$.
方法归纳——判断直线与圆相切的方法
(1)当直线和圆有一个公共点时,把圆心和这个公共点连接起来,然后证明直线垂直于这条半径,简称“连半径,证垂直”.
(2)当直线和圆的公共点没有明确时,可过圆心作直线的垂线,再证明圆心到直线的距离等于半径,简称“作垂直,证半径”.