第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
如图,在□ABCD中,对角线AC与BD相交于点F,AC⊥BD,且AC= 8,BD= 8√3.若P是对角线BD上一动点,连接AP,将AP绕点A按逆时针方向旋转至AE处,使得∠PAE= ∠BAD,连接PE,取AD的中点O,连接OE.在点P的运动过程中,线段OE长的最小值为______
2
.
答案:
2 解析:连接ED.
∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形.
∵AC=8,BD=8$\sqrt{3}$,
∴AF=$\frac{1}{2}$AC=4,DF=$\frac{1}{2}$BD=4$\sqrt{3}$,BA=DA.
∴AD=$\sqrt{AF²+DF²}$=8.
∴易得∠ADB=∠ABD=30°.
∵将AP绕点A按逆时针方向旋转至AE处,使得∠PAE=∠BAD,
∴AP=AE,∠BAP=∠DAE.在△BAP和△DAE中,{BA=DA,∠BAP=∠DAE,AP=AE},
∴△BAP≌△DAE.
∴∠ABP=∠ADE=30°.
∴DE是满足∠ADE=30°的线段.当OE⊥DE时,OE的长最小,
∵O是AD的中点,
∴OD=$\frac{1}{2}$AD=$\frac{1}{2}$×8=4.
∴OE=$\frac{1}{2}$OD=$\frac{1}{2}$×4=2.
∴在点P的运动过程中,线段OE长的最小值为2.
∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形.
∵AC=8,BD=8$\sqrt{3}$,
∴AF=$\frac{1}{2}$AC=4,DF=$\frac{1}{2}$BD=4$\sqrt{3}$,BA=DA.
∴AD=$\sqrt{AF²+DF²}$=8.
∴易得∠ADB=∠ABD=30°.
∵将AP绕点A按逆时针方向旋转至AE处,使得∠PAE=∠BAD,
∴AP=AE,∠BAP=∠DAE.在△BAP和△DAE中,{BA=DA,∠BAP=∠DAE,AP=AE},
∴△BAP≌△DAE.
∴∠ABP=∠ADE=30°.
∴DE是满足∠ADE=30°的线段.当OE⊥DE时,OE的长最小,
∵O是AD的中点,
∴OD=$\frac{1}{2}$AD=$\frac{1}{2}$×8=4.
∴OE=$\frac{1}{2}$OD=$\frac{1}{2}$×4=2.
∴在点P的运动过程中,线段OE长的最小值为2.
典例2 如图,在平面直角坐标系中,□OABC的顶点A的坐标为(4,0),点B的坐标为(6,2).
(1)□OABC的中心P的坐标为
(2)求点A,P所在直线对应的函数解析式.
(3)求证:不论k取何值,□OABC都被直线y= kx+1-3k分成面积相等的两部分.
(1)□OABC的中心P的坐标为
(3,1)
. (2)求点A,P所在直线对应的函数解析式.
设点A,P所在直线对应的函数解析式为y=mx+b,则{4m+b=0,3m+b=1},∴{m=−1,b=4}.∴点A,P所在直线对应的函数解析式为y=−x+4.
(3)求证:不论k取何值,□OABC都被直线y= kx+1-3k分成面积相等的两部分.
对于直线y=kx+1−3k,当x=3时,y=3k+1−3k=1,∴直线y=kx+1−3k经过点P(3,1).∴不论k取何值,□OABC都被直线y=kx+1−3k分成面积相等的两部分.
答案:
(1)(3,1).
(2)设点A,P所在直线对应的函数解析式为y=mx+b,则{4m+b=0,3m+b=1},
∴{m=−1,b=4}.
∴点A,P所在直线对应的函数解析式为y=−x+4.
(3)对于直线y=kx+1−3k,当x=3时,y=3k+1−3k=1,
∴直线y=kx+1−3k经过点P(3,1).
∴不论k取何值,□OABC都被直线y=kx+1−3k分成面积相等的两部分.
(1)(3,1).
(2)设点A,P所在直线对应的函数解析式为y=mx+b,则{4m+b=0,3m+b=1},
∴{m=−1,b=4}.
∴点A,P所在直线对应的函数解析式为y=−x+4.
(3)对于直线y=kx+1−3k,当x=3时,y=3k+1−3k=1,
∴直线y=kx+1−3k经过点P(3,1).
∴不论k取何值,□OABC都被直线y=kx+1−3k分成面积相等的两部分.
[变式] 如图,正方形OABC的顶点B的坐标为(2,-2),D(m,0)(m>2)为x轴上的一个动点,以BD为边作正方形BDEF,点E在第四象限.
(1)线段CD的长为______(用含m的代数式表示).
(2)试判断线段AD与CF之间的数量关系,并说明理由.
(3)设正方形BDEF的对称中心为点M,直线CM交y轴于点G,随着点D的运动,点G的位置是否会发生变化?若保持不变,请求出点G的坐标;若发生变化,请说明理由.
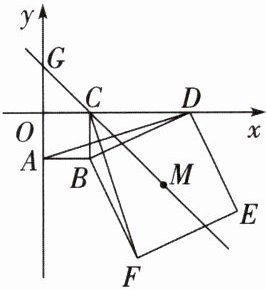
(1)线段CD的长为______(用含m的代数式表示).
(2)试判断线段AD与CF之间的数量关系,并说明理由.
(3)设正方形BDEF的对称中心为点M,直线CM交y轴于点G,随着点D的运动,点G的位置是否会发生变化?若保持不变,请求出点G的坐标;若发生变化,请说明理由.

答案:
(1)m−2.
(2)AD=CF.
理由:
∵四边形OABC和四边形BDEF都是正方形,
∴AB=CB,BD=BF,∠ABC=∠FBD=90°.
∴∠ABD=∠CBF.
∴△ABD≌△CBF.
∴AD=CF.
(3)点G的位置保持不变.
如图,过点F作FH⊥CB,交CB的延长线于点H,过点M作MN⊥x轴,垂足为N.
∵∠BCD=∠DBF=∠H=90°,
∴∠CBD+∠FBH=90°,∠FBH+∠HFB=90°.
∴∠CBD=∠HFB.
∵BD=FB,
∴△BCD≌△FHB.
∴CD=HB=m−2,BC=FH=2.
∴F(4,−m).
∵D(m,0),点M是正方形BDEF 的对称中心,
∴M(2+$\frac{m}{2}$,−$\frac{m}{2}$).
在△CMN中,MN=$\frac{m}{2}$,CN=$\frac{m}{2}$,
∴△CMN是等腰直角三角形.
∴∠OCG=∠NCM=45°.
∴△OCG也是等腰直角三角形.
∴OG=OC=2.
∴G(0,2).

(1)m−2.
(2)AD=CF.
理由:
∵四边形OABC和四边形BDEF都是正方形,
∴AB=CB,BD=BF,∠ABC=∠FBD=90°.
∴∠ABD=∠CBF.
∴△ABD≌△CBF.
∴AD=CF.
(3)点G的位置保持不变.
如图,过点F作FH⊥CB,交CB的延长线于点H,过点M作MN⊥x轴,垂足为N.
∵∠BCD=∠DBF=∠H=90°,
∴∠CBD+∠FBH=90°,∠FBH+∠HFB=90°.
∴∠CBD=∠HFB.
∵BD=FB,
∴△BCD≌△FHB.
∴CD=HB=m−2,BC=FH=2.
∴F(4,−m).
∵D(m,0),点M是正方形BDEF 的对称中心,
∴M(2+$\frac{m}{2}$,−$\frac{m}{2}$).
在△CMN中,MN=$\frac{m}{2}$,CN=$\frac{m}{2}$,
∴△CMN是等腰直角三角形.
∴∠OCG=∠NCM=45°.
∴△OCG也是等腰直角三角形.
∴OG=OC=2.
∴G(0,2).

典例3 如图,在平面直角坐标系中,点A的坐标为(-8,0),点B的坐标为(-4,3),将△OAB绕点O按顺时针方向旋转得到△OCD,点A的对应点C刚好落在AB的延长线上,则点B的对应点D的坐标为______.


答案:
(4,3) 解析:如图,连接BD,交y轴于点E,过点B作BF⊥x轴于点F.由旋转,得∠AOC=∠BOD,OC=OA,OD=OB.
∴∠OAC=∠OCA=$\frac{1}{2}$(180°−∠AOC), ∠OBD=∠ODB =$\frac{1}{2}$(180°−∠BOD).
∴∠OAC=∠OBD.
∵A(−8,0),B(−4,3),
∴OA=8,OF=4,
∴AF=OA−OF=4.
∴AF=OF=4.
∴BF垂直平分OA,
∴AB=OB.
∴∠OAC=∠AOB.
∴ ∠AOB =∠OBD.
∴BD//x轴.
∴OE⊥BD.
∴DE=BE.
∵B(−4,3),
∴BE=4,OE=3.
∴DE=4.
∴点D的坐标为(4,3).

(4,3) 解析:如图,连接BD,交y轴于点E,过点B作BF⊥x轴于点F.由旋转,得∠AOC=∠BOD,OC=OA,OD=OB.
∴∠OAC=∠OCA=$\frac{1}{2}$(180°−∠AOC), ∠OBD=∠ODB =$\frac{1}{2}$(180°−∠BOD).
∴∠OAC=∠OBD.
∵A(−8,0),B(−4,3),
∴OA=8,OF=4,
∴AF=OA−OF=4.
∴AF=OF=4.
∴BF垂直平分OA,
∴AB=OB.
∴∠OAC=∠AOB.
∴ ∠AOB =∠OBD.
∴BD//x轴.
∴OE⊥BD.
∴DE=BE.
∵B(−4,3),
∴BE=4,OE=3.
∴DE=4.
∴点D的坐标为(4,3).

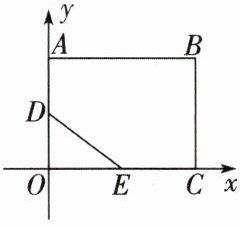
[变式] 分类讨论思想 如图,在平面直角坐标系中,矩形OABC的顶点坐标分别为O(0,0),A(0,6),B(8,6),C(8,0).点D(0,3)在OA上,点E(4,0)在OC上,连接DE.若将△DOE绕点O逆时针旋转,旋转角为α(0°<α<360°),得到△D'OE',连接AD',当∠AD'O= 90°时.
(1)α= ______.
(2)求点D',E'的坐标.
(1)α= ______.
(2)求点D',E'的坐标.

答案:
(1)60°或300°. 解析:如图①,连接DD'.当∠AD'O=90°时,DD'=AD=DO=$\frac{1}{2}$AO=3.
∵DO=D'O=3,
∴DO=D'O=DD'.
∴∠DOD'=60°.
∴α=60°.如图②,连接DD',当∠AD'O=90°时,DD'=AD=DO=$\frac{1}{2}$AO=3.
∵DO=OD',
∴DO=OD'=DD'
∴∠DOD'=60°.
∴α=360°−60°=300°.综上所述,α=60°或300°.
(2)如图①,作D'F⊥x轴于点F,E'H⊥x轴于点H.
∵∠AD'O=90°,∠AOD'=60°,
∴∠D'AO=30°,∠D'OF=30°.
∴∠E'OH=60°.
∵OD'=OD=3,OE'=OE=4,
∴易得D'F=$\frac{3}{2}$,FO=$\frac{3\sqrt{3}}{2}$,OH=2,E'H=2$\sqrt{3}$.
∴D'(−$\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$),E′(2,2$\sqrt{3}$)
如图②,同理,易得D'($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$),E'(2,−2$\sqrt{3}$).
综上所述,D'(−$\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$),E′(2,2$\sqrt{3}$)或D'($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$),E'(2,−2$\sqrt{3}$).


(1)60°或300°. 解析:如图①,连接DD'.当∠AD'O=90°时,DD'=AD=DO=$\frac{1}{2}$AO=3.
∵DO=D'O=3,
∴DO=D'O=DD'.
∴∠DOD'=60°.
∴α=60°.如图②,连接DD',当∠AD'O=90°时,DD'=AD=DO=$\frac{1}{2}$AO=3.
∵DO=OD',
∴DO=OD'=DD'
∴∠DOD'=60°.
∴α=360°−60°=300°.综上所述,α=60°或300°.
(2)如图①,作D'F⊥x轴于点F,E'H⊥x轴于点H.
∵∠AD'O=90°,∠AOD'=60°,
∴∠D'AO=30°,∠D'OF=30°.
∴∠E'OH=60°.
∵OD'=OD=3,OE'=OE=4,
∴易得D'F=$\frac{3}{2}$,FO=$\frac{3\sqrt{3}}{2}$,OH=2,E'H=2$\sqrt{3}$.
∴D'(−$\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$),E′(2,2$\sqrt{3}$)
如图②,同理,易得D'($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$),E'(2,−2$\sqrt{3}$).
综上所述,D'(−$\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$),E′(2,2$\sqrt{3}$)或D'($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$),E'(2,−2$\sqrt{3}$).


查看更多完整答案,请扫码查看


