《2025年拔尖特训九年级数学上册人教版》

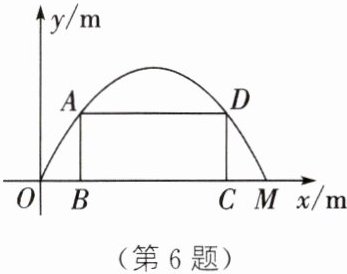
6. 施工队要修建一个横断面为抛物线形的公路隧道,其高度为8 m,宽度OM为16 m. 现以O为原点,OM所在直线为x轴建立如图所示的平面直角坐标系.
(1)求抛物线对应的函数解析式,并写出自变量x的取值范围.
(2)隧道下的公路是双向行车道(正中间是一条宽1 m的隔离带),其中的一条行车道能否行驶宽为3.5 m、高为5.8 m的车？
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使点A,D在抛物线上,点B,C在地面OM上. 为了筹备材料,需求出“脚手架”三根木杆AB,AD,DC的长度之和的最大值.

答案： （1）$\because$ 易知抛物线的顶点坐标为$(8,8)$，
$\therefore$ 设抛物线对应的函数解析式为$y=a(x-8)^{2}+8$.
将$O(0,0)$代入，得$0=64a+8$，解得$a=-\frac{1}{8}$.
$\therefore$ 抛物线对应的函数解析式为$y=-\frac{1}{8}(x-8)^{2}+8$，即$y= -\frac{1}{8}x^{2}+2x(0\leqslant x\leqslant16)$.
（2）$\because$ 双向行车道，且正中间是一条宽$1\ m$的隔离带，
$\therefore$ 每条行车道宽为$7.5\ m$，车沿着隔离带边沿行驶时，车另一侧边沿与隧道边沿的最近水平距离为$7.5- 3.5=4(m)$.
当$x=4$时，$y=-\frac{1}{8}x^{2}+2x=6$.
$\because 5.8＜6$，
$\therefore$ 其中的一条行车道能行驶宽为$3.5\ m$、高为$5.8\ m$的车.
（3）设$B(m,0)$，则$A\left(m,-\frac{1}{8}m^{2}+ 2m\right)$.
$\because$ 四边形$ABCD$是矩形，
$\therefore AB=DC$，$BC=AD$.
$\because$ 抛物线的对称轴为直线$x=8$，
$\therefore BC=AD=2(8-m)=(16-2m)m$.
设$AB$，$AD$，$DC$的长度之和为$w\ m$.
$\therefore w=16-2m+2\left(-\frac{1}{8}m^{2}+2m\right)= -\frac{1}{4}m^{2}+2m+16=-\frac{1}{4}(m- 4)^{2}+20$.
$\because -\frac{1}{4}＜0$，
$\therefore$ 当$m=4$时，$w$的最大值为$20$，即$AB$，$AD$，$DC$的长度之和的最大值是$20\ m$.

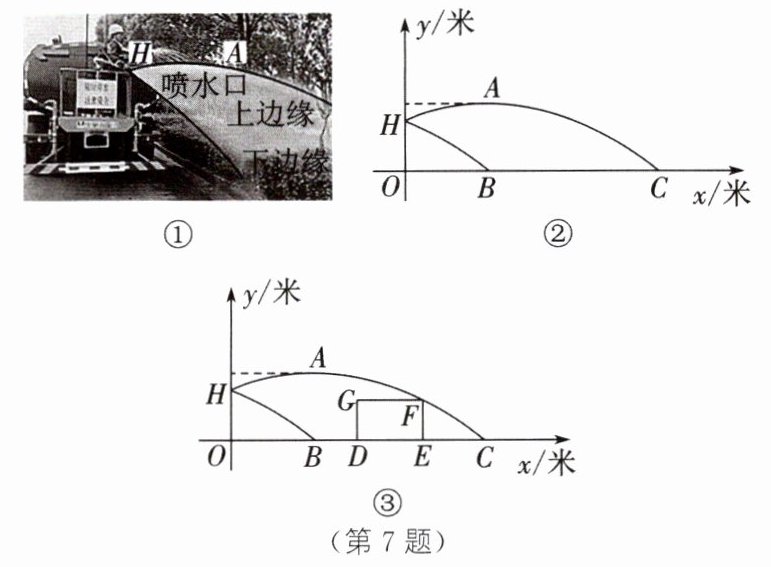
7. 新考法·项目式学习 如图①,一辆洒水车正在沿着公路行驶(平行于绿化带),为绿化带浇水. 数学小组想了解洒水车要如何把控行驶路线与绿化带之间的距离,才能保证喷出的水能浇灌到整个绿化带. 围绕这个问题,该小组开展了项目式学习. 建立如图②所示的平面直角坐标系,可以把洒水车喷出水的上、下边缘抽象为两条抛物线. 已知喷水口H离地面竖直高度为1.2米,上边缘抛物线最高点A离喷水口的水平距离为2米,高出喷水口0.4米.
(1)求上边缘抛物线对应的函数解析式.
(2)当喷头竖直高度调整时,喷头喷出的水柱形状不发生改变,即下边缘抛物线是由上边缘抛物线向左平移得到的. 如图③,把绿化带横截面抽象为矩形DEFG,其水平宽度DE= 1.8米,竖直高度EF= 1.1米,洒水车到绿化带的距离OD为d米.
①求下边缘抛物线与x轴的交点B的坐标.
②若d= 2.2,则洒水车行驶时喷出的水能能否浇灌到整个绿化带？请判断并说明理由.

答案： （1）由题意，得$A(2,1.6)$为上边缘抛物线的顶点.
设$y=a(x-2)^{2}+1.6$.
又$\because$ 上边缘抛物线过点$H(0,1.2)$，
$\therefore 1.2=4a+1.6$，解得$a=-0.1$.
$\therefore$ 上边缘抛物线对应的函数解析式为$y=-0.1(x-2)^{2}+1.6$.
（2）①$\because y=-0.1(x-2)^{2}+1.6$，
$\therefore$ 上边缘抛物线的对称轴为直线$x=2$.
$\therefore$ 点$(0,1.2)$关于对称轴的对称点为$(4,1.2)$.
$\therefore$ 下边缘抛物线是由上边缘抛物线向左平移$4$米得到的.
当$y=0$时，$0=-0.1(x-2)^{2}+1.6$，解得$x_{1}=6$，$x_{2}=-2$（舍去）.
$\therefore C(6,0)$.
$\therefore$ 点$B$的坐标为$(2,0)$.
②能.
理由：$\because DE=1.8$米，$EF=1.1$米，$OD=2.2$米，
$\therefore OE=2.2+1.8=4$（米）.
$\therefore$ 点$F$的坐标为$(4,1.1)$.
当$x=4$时，$y=-0.1×(4-2)^{2}+ 1.6=1.2$.
$\because 1.2＞1.1$，当$x＞2$时，$y$随$x$的增大而减小，
$\therefore$ 洒水车行驶时喷出的水能浇灌到整个绿化带.