《2025年53天天练六年级数学上册人教版》

4 为了方便运输,工作人员将羽毛球筒如图摆放,然后用绳子捆扎一圈,打结处需要10cm长的绳子。一根1.2m长的绳子,最多可以捆扎多少个羽毛球筒？

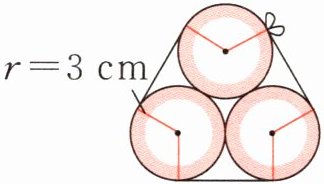
答案： $1.2\ \text{m}=120\ \text{cm}$
$2×3.14×3+3×6+10=46.84(\text{cm})$
$120÷46.84\approx2(\text{捆})$$2×3=6(\text{个})$
答：最多可以捆扎6个羽毛球筒。
解析 步骤一 求出捆扎3个羽毛球筒需要的绳子长度。观察题图可知，所需绳子长度为1个圆的周长加3条直径再加上打结处的长度，求得结果为46.84cm。
步骤二 求出1.2m里有多少个46.84cm。先换算单位，再用除法计算，这是一个实际问题，需要用“去尾法”保留整数。

5 泉城广场地处山、泉、河、城怀抱之中,是济南的标志性建筑之一。现在泉城广场运来了一批用于装饰的石柱,石柱横截面的半径都是0.5m。工人师傅要把其中一根石柱滚动着运到墙角堆放(如下图),这根石柱要滚动几圈？

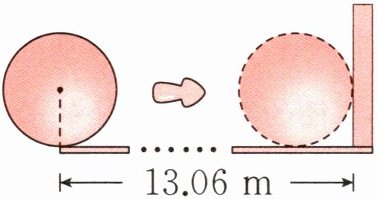
答案： $13.06-0.5=12.56(\text{m})$$2×3.14×0.5=3.14(\text{m})$
$12.56÷3.14=4(\text{圈})$
答：这根石柱要滚动4圈。
解析 步骤一 确定石柱滚动的距离。石柱滚动的距离=石柱横截面的圆心移动的距离=13.06m-石柱横截面的半径。
步骤二 求石柱横截面的周长。利用$C=2\pi r$计算。
步骤三 求石柱要滚动几圈。圈数=石柱滚动的距离÷石柱横截面的周长。

6 某商场里有以下三款折叠桌。(π取3)

(1)A款折叠桌展开后比折叠时的面积增加了多少？
(2)B款折叠桌折叠后的面积是多少？
(3)C款折叠桌展开后的面积是多少？

答案： （1）折叠时：$2×2=4(\text{m}^{2})$
展开后：$3×(4÷4×2)=6(\text{m}^{2})$
$6-4=2(\text{m}^{2})$
答：A款折叠桌展开后比折叠时的面积增加了$2\ \text{m}^{2}$。
解析 用圆的面积减正方形的面积可得增加的面积。设圆的半径为r，正方形的面积等于4个以半径为底、以半径为高的三角形的面积之和，即$\frac{1}{2}× r^{2}×4=4$，则$r^{2}=4÷4×2$，从而求出圆的面积。
（2）$3×1.5^{2}÷4-1.5×1.5÷2=0.5625(\text{m}^{2})$
$3×1.5^{2}-0.5625×2=5.625(\text{m}^{2})$
答：B款折叠桌折叠后的面积是$5.625\ \text{m}^{2}$。
解析 用圆的面积减去上、下折叠的面积可得折叠后的面积。上、下折叠的面积=$2×\left(\frac{1}{4}\text{圆的面积}-\text{直角边为1.5 m的等腰直角三角形的面积}\right)$。
（3）$3×(3÷2)^{2}+0.5×3=8.25(\text{m}^{2})$
答：C款折叠桌展开后的面积是$8.25\ \text{m}^{2}$。
解析 2个半圆的面积加上中间长方形的面积可得展开后的面积。

7 鲁克洛斯三角形是一种特殊的三角形,它是分别以等边三角形的三个顶点为圆心、以其边长为半径作圆弧,由这三段圆弧组成的曲边三角形(如图)。

(1)请你以等边三角形ABC的三个顶点为圆心,画出一个鲁克洛斯三角形。

(2)如果等边三角形的边长是5cm,那么鲁克洛斯三角形的周长是多少厘米？

答案：
（1）

解析 根据题干描述作图即可。
（2）$2×3.14×5×\frac{180}{360}=15.7(\text{cm})$
答：鲁洛克斯三角形的周长是15.7 cm。
解析 鲁洛克斯三角形的周长是3个半径为5 cm、圆心角为$60^{\circ}$的扇形对应的弧的长度之和，也就是半径为5 cm、圆心角为$180^{\circ}$的扇形对应的弧的长度。