第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
21. (8分)阅读与计算:请阅读以下材料,并完成相应的任务。
古希腊的几何学家海伦在他的《度量》一书中给出了利用三角形的三边求三角形面积的“海伦公式”:若一个三角形的三边长分别为$a,b,c$,设$p = \frac {a + b + c}{2}$,则三角形的面积$S = \sqrt {p(p - a)(p - b)(p - c)}$。
我国南宋著名的数学家秦九韶,曾提出利用三角形的三边求面积的“秦九韶公式”(三斜求积术):若一个三角形的三边长分别为$a,b,c$,
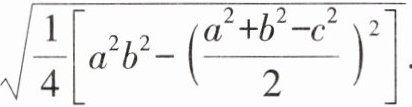
则三角形的面积$S = \sqrt {\frac {1}{4}[a^{2}b^{2} - (\frac {a^{2} + b^{2} - c^{2}}{2})^{2}]}$。
(1)若一个三角形的三边长分别是5,6,7,则这个三角形的面积等于____;
(2)若一个三角形的三边长分别是$\sqrt {5},\sqrt {6},\sqrt {7}$,求这个三角形的面积。
古希腊的几何学家海伦在他的《度量》一书中给出了利用三角形的三边求三角形面积的“海伦公式”:若一个三角形的三边长分别为$a,b,c$,设$p = \frac {a + b + c}{2}$,则三角形的面积$S = \sqrt {p(p - a)(p - b)(p - c)}$。
我国南宋著名的数学家秦九韶,曾提出利用三角形的三边求面积的“秦九韶公式”(三斜求积术):若一个三角形的三边长分别为$a,b,c$,
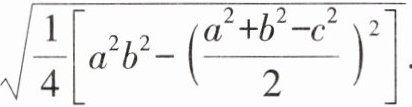
则三角形的面积$S = \sqrt {\frac {1}{4}[a^{2}b^{2} - (\frac {a^{2} + b^{2} - c^{2}}{2})^{2}]}$。
(1)若一个三角形的三边长分别是5,6,7,则这个三角形的面积等于____;
(2)若一个三角形的三边长分别是$\sqrt {5},\sqrt {6},\sqrt {7}$,求这个三角形的面积。
答案:
(1)$6\sqrt{6}$ 解析:$p=\frac{a + b + c}{2}=\frac{5 + 6 + 7}{2}=9$,$S=\sqrt{p(p - a)(p - b)(p - c)}=\sqrt{9\times(9 - 5)\times(9 - 6)\times(9 - 7)}=6\sqrt{6}$。故这个三角形的面积等于$6\sqrt{6}$。
(2)$S=\sqrt{\frac{1}{4}[a^{2}b^{2}-(\frac{a^{2}+b^{2}-c^{2}}{2})^{2}]}=\sqrt{\frac{1}{4}\times\{(\sqrt{5})^{2}\times(\sqrt{6})^{2}-[\frac{(\sqrt{5})^{2}+(\sqrt{6})^{2}-(\sqrt{7})^{2}}{2}]^{2}\}}=\sqrt{\frac{1}{4}\times[5\times 6 - (\frac{5 + 6 - 7}{2})^{2}]}=\sqrt{\frac{1}{4}\times(30 - 4)}=\frac{\sqrt{26}}{2}$。
故这个三角形的面积是$\frac{\sqrt{26}}{2}$。
(1)$6\sqrt{6}$ 解析:$p=\frac{a + b + c}{2}=\frac{5 + 6 + 7}{2}=9$,$S=\sqrt{p(p - a)(p - b)(p - c)}=\sqrt{9\times(9 - 5)\times(9 - 6)\times(9 - 7)}=6\sqrt{6}$。故这个三角形的面积等于$6\sqrt{6}$。
(2)$S=\sqrt{\frac{1}{4}[a^{2}b^{2}-(\frac{a^{2}+b^{2}-c^{2}}{2})^{2}]}=\sqrt{\frac{1}{4}\times\{(\sqrt{5})^{2}\times(\sqrt{6})^{2}-[\frac{(\sqrt{5})^{2}+(\sqrt{6})^{2}-(\sqrt{7})^{2}}{2}]^{2}\}}=\sqrt{\frac{1}{4}\times[5\times 6 - (\frac{5 + 6 - 7}{2})^{2}]}=\sqrt{\frac{1}{4}\times(30 - 4)}=\frac{\sqrt{26}}{2}$。
故这个三角形的面积是$\frac{\sqrt{26}}{2}$。
22. (10分)在进行二次根式化简时,我们有时会碰上如$\frac {3}{\sqrt {5}},\sqrt {\frac {2}{3}},\frac {2}{\sqrt {3} + 1}$这样的式子,其实我们还可以将其进一步化简,例如:
$\frac {3}{\sqrt {5}} = \frac {3×\sqrt {5}}{\sqrt {5}×\sqrt {5}} = \frac {3\sqrt {5}}{5}$; ①
$\sqrt {\frac {2}{3}} = \sqrt {\frac {2×3}{3×3}} = \frac {\sqrt {6}}{3}$; ②
$\frac {2}{\sqrt {3} + 1} = \frac {2(\sqrt {3} - 1)}{(\sqrt {3} + 1)(\sqrt {3} - 1)} = \frac {2(\sqrt {3} - 1)}{(\sqrt {3})^{2} - 1^{2}} = \sqrt {3} - 1$。 ③
以上这种化简的步骤叫做分母有理化。
$\frac {2}{\sqrt {3} + 1}$还可以用以下方法化简:
$\frac {2}{\sqrt {3} + 1} = \frac {3 - 1}{\sqrt {3} + 1} = \frac {(\sqrt {3})^{2} - 1^{2}}{\sqrt {3} + 1} = \frac {(\sqrt {3} + 1)(\sqrt {3} - 1)}{\sqrt {3} + 1} = \sqrt {3} - 1$。 ④
(1)参照③式化简:$\frac {2}{\sqrt {5} + \sqrt {3}}$;
(2)参照④式化简:$\frac {2}{\sqrt {5} + \sqrt {3}}$;
(3)化简:$\frac {1}{\sqrt {3} + 1} + \frac {1}{\sqrt {5} + \sqrt {3}} + \frac {1}{\sqrt {7} + \sqrt {5}} + … + \frac {1}{\sqrt {2n + 1} + \sqrt {2n - 1}}$。
$\frac {3}{\sqrt {5}} = \frac {3×\sqrt {5}}{\sqrt {5}×\sqrt {5}} = \frac {3\sqrt {5}}{5}$; ①
$\sqrt {\frac {2}{3}} = \sqrt {\frac {2×3}{3×3}} = \frac {\sqrt {6}}{3}$; ②
$\frac {2}{\sqrt {3} + 1} = \frac {2(\sqrt {3} - 1)}{(\sqrt {3} + 1)(\sqrt {3} - 1)} = \frac {2(\sqrt {3} - 1)}{(\sqrt {3})^{2} - 1^{2}} = \sqrt {3} - 1$。 ③
以上这种化简的步骤叫做分母有理化。
$\frac {2}{\sqrt {3} + 1}$还可以用以下方法化简:
$\frac {2}{\sqrt {3} + 1} = \frac {3 - 1}{\sqrt {3} + 1} = \frac {(\sqrt {3})^{2} - 1^{2}}{\sqrt {3} + 1} = \frac {(\sqrt {3} + 1)(\sqrt {3} - 1)}{\sqrt {3} + 1} = \sqrt {3} - 1$。 ④
(1)参照③式化简:$\frac {2}{\sqrt {5} + \sqrt {3}}$;
(2)参照④式化简:$\frac {2}{\sqrt {5} + \sqrt {3}}$;
(3)化简:$\frac {1}{\sqrt {3} + 1} + \frac {1}{\sqrt {5} + \sqrt {3}} + \frac {1}{\sqrt {7} + \sqrt {5}} + … + \frac {1}{\sqrt {2n + 1} + \sqrt {2n - 1}}$。
答案:
(1)$\frac{2}{\sqrt{5}+\sqrt{3}}=\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}=\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5})^{2}-(\sqrt{3})^{2}}=\sqrt{5}-\sqrt{3}$。
(2)$\frac{2}{\sqrt{5}+\sqrt{3}}=\frac{(\sqrt{5})^{2}-(\sqrt{3})^{2}}{\sqrt{5}+\sqrt{3}}=\frac{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}{\sqrt{5}+\sqrt{3}}=\sqrt{5}-\sqrt{3}$。
(3)原式$=\frac{\sqrt{3}-1}{2}+\frac{\sqrt{5}-\sqrt{3}}{2}+\frac{\sqrt{7}-\sqrt{5}}{2}+\cdots+\frac{\sqrt{2n + 1}-\sqrt{2n - 1}}{2}=\frac{\sqrt{2n + 1}-1}{2}$。
(1)$\frac{2}{\sqrt{5}+\sqrt{3}}=\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}=\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5})^{2}-(\sqrt{3})^{2}}=\sqrt{5}-\sqrt{3}$。
(2)$\frac{2}{\sqrt{5}+\sqrt{3}}=\frac{(\sqrt{5})^{2}-(\sqrt{3})^{2}}{\sqrt{5}+\sqrt{3}}=\frac{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}{\sqrt{5}+\sqrt{3}}=\sqrt{5}-\sqrt{3}$。
(3)原式$=\frac{\sqrt{3}-1}{2}+\frac{\sqrt{5}-\sqrt{3}}{2}+\frac{\sqrt{7}-\sqrt{5}}{2}+\cdots+\frac{\sqrt{2n + 1}-\sqrt{2n - 1}}{2}=\frac{\sqrt{2n + 1}-1}{2}$。
查看更多完整答案,请扫码查看


