《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

14. 不等式组$\begin{cases}3x - 9 ＞ 0, \\ x ＞ k + 1\end{cases}的解集为x ＞ 3$,则$k$的取值范围为______.

答案： $ k \leq 2 $

15. 若干名学生住宿舍,若每间住$4$人,则$2$人无处住;若每间住$6$人,则空一间还有一间不空也不满,问有多少名学生和多少间宿舍?设有$x$间宿舍,则可列不等式(组)为______.

答案： $ \begin{cases} 4x + 2 - 6(x - 2) \geq 1, \\ 4x + 2 - 6(x - 2) \leq 5 \end{cases} $

16. 按如下程序进行运算,并规定,程序运行到“结果是否大于$65$”为一次运算,且运算进行$4$次才停止.则可输入的整数$x$的个数是______.

答案： 4 解析:根据题意得第一次:$ 2x - 1 $,第二次:$ 2(2x - 1) - 1 = 4x - 3 $,第三次:$ 2(4x - 3) - 1 = 8x - 7 $,第四次:$ 2(8x - 7) - 1 = 16x - 15 $,根据题意得$ \begin{cases} 2x - 1 \leq 65, \\ 4x - 3 \leq 65, \\ 8x - 7 \leq 65, \\ 16x - 15 ＞ 65, \end{cases} $
解得$ 5 ＜ x \leq 9 $,则x的整数值是6,7,8,9.共有4个.

17. (8分)(1)解不等式:$3(x + 2) - 1 \leq 11 - 2(x - 2)$;
(2)解不等式组$\begin{cases}2 - x ＞ 0, \\ \frac{5x + 1}{2} + 1 \geq \frac{2x - 1}{3}.\end{cases}$

答案：
(1)$ x \leq 2 $
(2)$ -1 \leq x ＜ 2 $

18. (8分)若不等式$\frac{x + 5}{2} - 1 ＜ \frac{ax + 2}{2}的解集与不等式2x - 1 ＞ 0$的解集相同,试确定$a$的取值.

答案： 解$ 2x - 1 ＞ 0 $,得$ x ＞ \frac{1}{2} $.
∵不等式$ \frac{x + 5}{2} - 1 ＜ \frac{ax + 2}{2} $的解集与不等式$ 2x - 1 ＞ 0 $的解集相同,
∴$ \frac{x + 5}{2} - 1 ＜ \frac{ax + 2}{2} $的解集应为$ x ＞ \frac{1}{a - 1} $.
∴$ \frac{1}{a - 1} = \frac{1}{2} $,解得$ a = 3 $,符合题意.

19. (8分)若方程组$\begin{cases}2x + y = 2k, \\ x - y = -2\end{cases}的解满足x ＜ 1且y ＞ 1$,求$k$的取值范围.

答案： 解方程组得$ \begin{cases} x = \frac{2k - 2}{3}, \\ y = \frac{2k + 4}{3}. \end{cases} $又
∵$ x ＜ 1 $且$ y ＞ 1 $,
∴$ \begin{cases} \frac{2k - 2}{3} ＜ 1, \\ \frac{2k + 4}{3} ＞ 1, \end{cases} $
解得$ -\frac{1}{2} ＜ k ＜ \frac{5}{2} $.

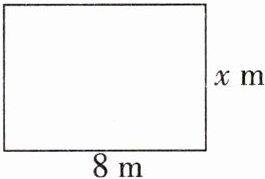
20. (8分)某小区前面有一块空地,现想建成一块面积大于$48m^{2}$、周长小于$34m$的长方形绿化草地(如图),已知一边长为$8m$,设其邻边长为$x m$,求$x$的整数解.

答案： 依题意,得$ \begin{cases} 8x ＞ 48, \\ 2(x + 8) ＜ 34, \end{cases} $解得$ 6 ＜ x ＜ 9 $,
∴x的整数解为7,8.