《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

18. (8分)在如图所示的网格中,每个小正方形的边长均为1个单位.

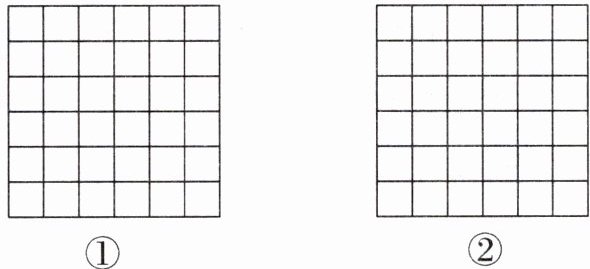
(1)请你在图①中画一个以格点为顶点,面积为6个平方单位的等腰三角形；
(2)请你在图②中画一个以格点为顶点,三边都不与网格线重合的直角三角形.

答案： 作图略，答案不唯一。

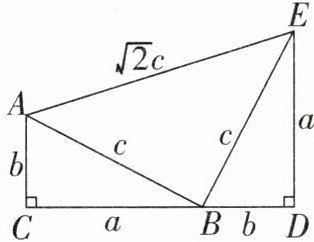
19. (8分)如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED的边长,易知AE= $\sqrt{2}c$,这时我们把关于x的形如$ax^2+\sqrt{2}cx+b= 0$的一元二次方程称为“勾系一元二次方程”.若x= -1是“勾系一元二次方程”$ax^2+\sqrt{2}cx+b= 0$的一个根,且四边形ACDE的周长是$6\sqrt{2}$,求△ABC的面积.

答案： 当x = -1时,有a - $\sqrt{2}$c + b = 0，即a + b = $\sqrt{2}$c。
∵2a + 2b + $\sqrt{2}$c = 6$\sqrt{2}$，即2(a + b) + $\sqrt{2}$c = 6$\sqrt{2}$，
∴3$\sqrt{2}$c = 6$\sqrt{2}$，
∴c = 2，
∴a² + b² = c² = 4，a + b = 2$\sqrt{2}$。
∵(a + b)² = a² + b² + 2ab，
∴ab = 2，
∴S_{△ABC} = $\frac{1}{2}$ab = 1。

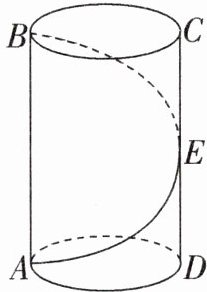
20. (10分)一只螳螂在一圆柱形松树树干的A点处,发现它的正上方B点处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是按如图所示的路线,绕到虫子后面吃掉它.已知树干的周长为20cm,A,B两点间的距离为15cm.若螳螂想吃掉在B点的小虫子,求螳螂绕行的最短路程.

答案：
把这段树干看成用纸卷成的圆柱，从AB处将它展开如下:
　　　　　　　　
　则AB即为所求的最短距离，其中BM = 15cm,AM = 20cm。在Rt△AMB中,AB = $\sqrt{AM² + BM²}$ = $\sqrt{15² + 20²}$ = 25(cm)。
　故螳螂绕行的最短路程是25cm。

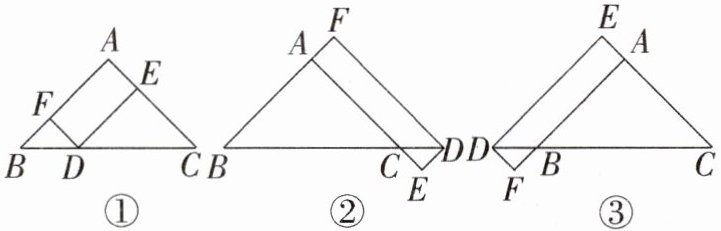
21. (10分)在Rt△ABC中,AB= AC,点D在边BC所在的直线上,过点D作DF//AC交直线AB于点F,DE//AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证：$DE+DF= \frac{\sqrt{2}}{2}BC$；
(2)当点D在边BC的延长线上时(如图②)或当点D在边BC的反向延长线上时(如图③),线段DE,DF,BC又有怎样的数量关系？请直接写出你的猜想,并选择其中一种情况加以证明.

答案：
(1)
∵DF//AC,DE//AB,
∴四边形AFDE是平行四边形。
∵在Rt△ABC中,AB = AC,
∴∠A = 90°,∠B = ∠C = 45°,
∴▱AFDE是矩形,
∴∠AFD = ∠AED = 90°,
∴∠BFD = ∠DEC = 90°,
∴△BDF和△DEC是等腰直角三角形，
∴BD = $\sqrt{2}$DF,CD = $\sqrt{2}$DE,
∴BC = BD + DC = $\sqrt{2}$(DE + DF),
∴DE + DF = $\frac{\sqrt{2}}{2}$BC。
(2)图②中:DF - DE = $\frac{\sqrt{2}}{2}$BC,图③中:DE - DF = $\frac{\sqrt{2}}{2}$BC。下面证明图②的情况:
∵在Rt△ABC中,AB = AC,
∴∠BAC = 90°,∠B = ∠ACB = 45°。
∵DF//AC,DE//AB,
∴∠F = ∠BAC = 90°,∠E = ∠BAC = 90°,∠CDE = ∠B = 45°,
∴△BDF和△DEC是等腰直角三角形，
∴BD = $\sqrt{2}$DF,CD = $\sqrt{2}$DE,
∴BC = BD - DC = $\sqrt{2}$(DF - DE),
∴DF - DE = $\frac{\sqrt{2}}{2}$BC。