《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

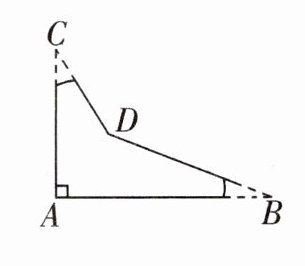
18. (8分)一个零件的形状如图所示,按规定$∠A应等于90^{\circ}$,$∠B和∠C应分别等于21^{\circ}和32^{\circ}$,现测量得$∠BDC= 148^{\circ}$,你认为这个零件合格吗？为什么？

答案：
如图，延长CD交AB于点F.
　则∠DFB = ∠C + ∠A = 32° + 90° = 122°，
　　　　　　　　　　　　　　　 ∠BDC = ∠DFB + ∠B = 122° + 21° = 143°，
　　即合格零件的∠BDC应为143°.
　而此零件测量得∠BDC = 148°，
∴这个零件不合格.

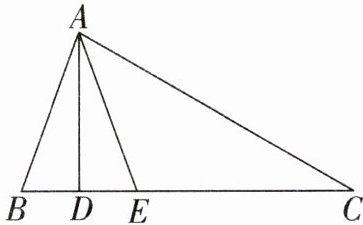
19. (8分)如图,在$\triangle ABC$中,$AD⊥BC$,垂足为$D$,$AE平分∠BAC$,$∠B= 70^{\circ}$,$∠C= 30^{\circ}$.
(1)求$∠BAE$的度数.
(2)求$∠DAE$的度数.
(3)探究：小明认为如果条件“$∠B= 70^{\circ}$,$∠C= 30^{\circ}$”改成“$∠B-∠C= 40^{\circ}$”,也能得出$∠DAE$的度数.若能,请你写出求解过程；若不能,请说明理由.

答案：
(1)
∵∠B + ∠C + ∠BAC = 180°，
∴∠BAC = 180° - ∠B - ∠C = 180° - 70° - 30° = 80°.
∵AE平分∠BAC，
∴∠BAE = $\frac{1}{2}$∠BAC = 40°.
(2)
∵AD⊥BC，
∴∠ADE = 90°.而∠ADE = ∠B + ∠BAD，
∴∠BAD = 90° - ∠B = 90° - 70° = 20°，
∴∠DAE = ∠BAE - ∠BAD = 40° - 20° = 20°.
(3)
∵∠B + ∠C + ∠BAC = 180°，
∴∠BAC = 180° - ∠B - ∠C.
∵AE平分∠BAC，
∴∠BAE = $\frac{1}{2}$∠BAC = $\frac{1}{2}$(180° - ∠B - ∠C) = 90° - $\frac{1}{2}$(∠B + ∠C).
∵AD⊥BC，
∴∠ADE = 90°.而∠ADE = ∠B + ∠BAD，
∴∠BAD = 90° - ∠B，
∴∠DAE = ∠BAE - ∠BAD = 90° - $\frac{1}{2}$(∠B + ∠C) - (90° - ∠B) = $\frac{1}{2}$(∠B - ∠C).
　
∵∠B - ∠C = 40°，
∴∠DAE = $\frac{1}{2}$×40° = 20°.

20. (10分)如图,公园有一条“$Z$”字形道路$ABCD$,其中$AB// CD$,在$E$,$M$,$F$处各有一个小石凳,且$BE= CF$,$M为BC$的中点,请问三个小石凳是否在一条直线上？说出你推断的理由.

答案： 三个小石凳在一条直线上.理由:连结EM并延长，交CD于点F'.因为M为BC的中点，所以BM = CM.因为AB//CD，所以∠B = ∠C，∠BEM = ∠CF'M.又因为BM = CM，所以△BEM≌△CF'M，所以BE = CF'.又因为BE = CF，所以CF' = CF，即点F'与点F重合.所以点E,M,F在一条直线上.