《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

1. 若实数 $ m,n $ 满足 $ |m - 2|+\sqrt{n - 4}= 0 $,且 $ m,n $ 恰好是等腰 $ \triangle ABC $ 的两条边的边长,则 $ \triangle ABC $ 的周长是()
A. 12
B. 10
C. 8
D. 6

答案： B

2. 如图,$ AB// CD $,$ AD// BC $.图中全等三角形共有()

A. 2 对
B. 3 对
C. 4 对
D. 5 对

答案： C

3. 如图,点 $ E $ 在正方形 $ ABCD $ 内,满足 $ \angle AEB = 90^{\circ} $,$ AE = 6 $,$ BE = 8 $,则阴影部分的面积是()

A. 48
B. 60
C. 76
D. 80

答案： C

4. 将一副三角板按图中方式叠放,则角 $ \alpha $ 等于()

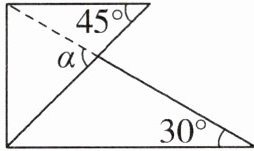
A. $ 30^{\circ} $
B. $ 45^{\circ} $
C. $ 60^{\circ} $
D. $ 75^{\circ} $

答案： D

5. 如图,已知点 $ P $ 是矩形 $ ABCD $ 内一点(不含边界),设 $ \angle PAD= \theta_1 $,$ \angle PBA= \theta_2 $,$ \angle PCB= \theta_3 $,$ \angle PDC= \theta_4 $,若 $ \angle APB = 80^{\circ} $,$ \angle CPD = 50^{\circ} $,则()

A. $ (\theta_1+\theta_4)-(\theta_2+\theta_3)= 30^{\circ} $
B. $ (\theta_2+\theta_4)-(\theta_1+\theta_3)= 40^{\circ} $
C. $ (\theta_1+\theta_2)-(\theta_3+\theta_4)= 70^{\circ} $
D. $ (\theta_1+\theta_2)+(\theta_3+\theta_4)= 180^{\circ} $

答案： A

6. 如图,在 $ \triangle ABC $ 中,延长 $ BC $ 至点 $ D $,使得 $ CD= \frac{1}{2}BC $,过 $ AC $ 的中点 $ E $ 作 $ EF// CD $(点 $ F $ 位于点 $ E $ 的右侧),且 $ EF = 2CD $,连结 $ DF $.若 $ AB = 8 $,则 $ DF $ 的长为()

A. 3
B. 4
C. $ 2\sqrt{3} $
D. $ 3\sqrt{2} $

答案： B

7. 如图,在正方形 $ ABCD $ 中,点 $ E,F $ 分别在 $ BC,CD $ 上,$ \triangle AEF $ 是等边三角形,连结 $ AC $ 交 $ EF $ 于点 $ G $,下列结论：① $ BE = DF $；② $ \angle DAF = 15^{\circ} $；③ $ AC $ 垂直平分 $ EF $；④ $ BE + DF = EF $；⑤ $ S_{\triangle CEF}= 2S_{\triangle ABE} $.其中正确的结论有()

A. 2 个
B. 3 个
C. 4 个
D. 5 个

答案： C

8. 如图,在五边形 $ ABCDE $ 中,$ \angle BAE = 120^{\circ} $,$ \angle B= \angle E = 90^{\circ} $,$ AB = BC $,$ AE = DE $,在 $ BC,DE $ 上分别找一点 $ M,N $,使得 $ \triangle AMN $ 的周长最小,则 $ \angle AMN+\angle ANM $ 的度数为()

A. $ 100^{\circ} $
B. $ 110^{\circ} $
C. $ 120^{\circ} $
D. $ 130^{\circ} $

答案： C