第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
21. (10分)若两个一次函数 $ y = k_1x + b_1(k_1 \neq 0) $,$ y = k_2x + b_2(k_2 \neq 0) $,则称函数 $ y = (k_1 + k_2)x + b_1b_2 $ 为这两个函数的“和谐函数”.
(1)求一次函数 $ y = 2x + 3 $ 与 $ y = -4x + 4 $ 的“和谐函数”的表达式,若此“和谐函数”的图象与 $ x $ 轴相交于点 $ A $,与 $ y $ 轴相交于点 $ B $,求 $ \triangle ABO $ 的面积;
(2)若一次函数 $ y = -ax + 1 $ 与 $ y = x - 2b $ 的“和谐函数”为 $ y = 4x + 3 $,则 $ a = $______,$ b = $______;
(3)已知一次函数 $ y = x + b $ 与 $ y = -kx + 5 $ 的“和谐函数”的图象经过第一、二、四象限,则常数 $ k $,$ b $ 满足的条件为 $ k $______1且 $ b $______0.(用“>”“=”或“<”填空)
(1)求一次函数 $ y = 2x + 3 $ 与 $ y = -4x + 4 $ 的“和谐函数”的表达式,若此“和谐函数”的图象与 $ x $ 轴相交于点 $ A $,与 $ y $ 轴相交于点 $ B $,求 $ \triangle ABO $ 的面积;
(2)若一次函数 $ y = -ax + 1 $ 与 $ y = x - 2b $ 的“和谐函数”为 $ y = 4x + 3 $,则 $ a = $______,$ b = $______;
(3)已知一次函数 $ y = x + b $ 与 $ y = -kx + 5 $ 的“和谐函数”的图象经过第一、二、四象限,则常数 $ k $,$ b $ 满足的条件为 $ k $______1且 $ b $______0.(用“>”“=”或“<”填空)
答案:
(1)由题意,得所求的“和谐函数”的表达式为$y=(2 - 4)x + 3\times4$,
即$y = - 2x + 12$。
令$x = 0$,得$y = 12$;令$y = 0$,得$x = 6$,
则$S_{\triangle ABO}=\frac{1}{2}\times6\times12 = 36$。
(2)$-3$ $-\frac{3}{2}$ 解析:根据题意,得$\begin{cases}-a + 1 = 4\\-2b = 3\end{cases}$,解得$\begin{cases}a = - 3\\b = -\frac{3}{2}\end{cases}$。
(3)$>$ $>$ 解析:根据题意,得$\begin{cases}1 - k < 0\\5b > 0\end{cases}$,解得$\begin{cases}k > 1\\b > 0\end{cases}$。
(1)由题意,得所求的“和谐函数”的表达式为$y=(2 - 4)x + 3\times4$,
即$y = - 2x + 12$。
令$x = 0$,得$y = 12$;令$y = 0$,得$x = 6$,
则$S_{\triangle ABO}=\frac{1}{2}\times6\times12 = 36$。
(2)$-3$ $-\frac{3}{2}$ 解析:根据题意,得$\begin{cases}-a + 1 = 4\\-2b = 3\end{cases}$,解得$\begin{cases}a = - 3\\b = -\frac{3}{2}\end{cases}$。
(3)$>$ $>$ 解析:根据题意,得$\begin{cases}1 - k < 0\\5b > 0\end{cases}$,解得$\begin{cases}k > 1\\b > 0\end{cases}$。
22. (10分)快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地. 慢车到达甲地比快车到达甲地早 $ \frac{1}{2} $ 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程 $ y $(千米)与所用时间 $ x $(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度.
(2)求快车返回过程中 $ y $(千米)与 $ x $(小时)的函数表达式.
(3)两车出发后经过多长时间相距90千米的路程?
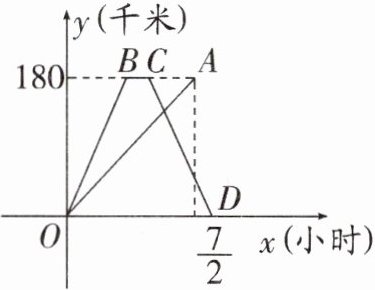
(1)请直接写出快、慢两车的速度.
(2)求快车返回过程中 $ y $(千米)与 $ x $(小时)的函数表达式.
(3)两车出发后经过多长时间相距90千米的路程?

答案:
(1)快车速度:120千米/时,慢车速度:60千米/时。
(2)快车停留的时间:$\frac{7}{2}-\frac{180}{120}\times2=\frac{1}{2}$(小时),
$\frac{1}{2}+\frac{180}{120}=2$(小时),
∴$C(2,180)$,
设直线$CD$的函数表达式为$y = kx + b$,将$C(2,180)$,$D(\frac{7}{2},0)$代入,得$\begin{cases}180 = 2k + b\\0 = \frac{7}{2}k + b\end{cases}$,解得$\begin{cases}k = - 120\\b = 420\end{cases}$,
∴快车返回过程中$y$(千米)与$x$(小时)的函数表达式为$y = - 120x + 420(2\leqslant x\leqslant\frac{7}{2})$。
(3)相遇之前:$120x + 60x + 90 = 180$,解得$x = \frac{1}{2}$;
相遇之后:$120x + 60x - 90 = 180$,解得$x = \frac{3}{2}$;
快车从甲地到乙地需要$180\div120=\frac{3}{2}$(小时),
快车返回之后:$60x = 90 + 120(x - \frac{1}{2}-\frac{3}{2})$,解得$x = \frac{5}{2}$。
综上所述,两车出发后经过$\frac{1}{2}$小时或$\frac{3}{2}$小时或$\frac{5}{2}$小时时相距90千米的路程。
(1)快车速度:120千米/时,慢车速度:60千米/时。
(2)快车停留的时间:$\frac{7}{2}-\frac{180}{120}\times2=\frac{1}{2}$(小时),
$\frac{1}{2}+\frac{180}{120}=2$(小时),
∴$C(2,180)$,
设直线$CD$的函数表达式为$y = kx + b$,将$C(2,180)$,$D(\frac{7}{2},0)$代入,得$\begin{cases}180 = 2k + b\\0 = \frac{7}{2}k + b\end{cases}$,解得$\begin{cases}k = - 120\\b = 420\end{cases}$,
∴快车返回过程中$y$(千米)与$x$(小时)的函数表达式为$y = - 120x + 420(2\leqslant x\leqslant\frac{7}{2})$。
(3)相遇之前:$120x + 60x + 90 = 180$,解得$x = \frac{1}{2}$;
相遇之后:$120x + 60x - 90 = 180$,解得$x = \frac{3}{2}$;
快车从甲地到乙地需要$180\div120=\frac{3}{2}$(小时),
快车返回之后:$60x = 90 + 120(x - \frac{1}{2}-\frac{3}{2})$,解得$x = \frac{5}{2}$。
综上所述,两车出发后经过$\frac{1}{2}$小时或$\frac{3}{2}$小时或$\frac{5}{2}$小时时相距90千米的路程。
查看更多完整答案,请扫码查看


