第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 已知$x^{2}= 3$,那么在数轴上与实数$x$对应的点可能是()
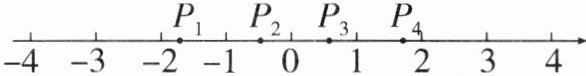
A. $P_{1}$
B. $P_{4}$
C. $P_{2}或P_{3}$
D. $P_{1}或P_{4}$
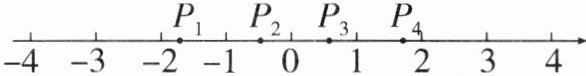
A. $P_{1}$
B. $P_{4}$
C. $P_{2}或P_{3}$
D. $P_{1}或P_{4}$
答案:
D
2. 计算$(-2)^{2025}+(-2)^{2026}$的值为()
A. 1
B. -1
C. $2^{2025}$
D. $-2^{2025}$
A. 1
B. -1
C. $2^{2025}$
D. $-2^{2025}$
答案:
C
3. 因式分解$x - 4x^{3}$的最后结果是()
A. $x(1 - 2x)^{2}$
B. $x(2x - 1)(2x + 1)$
C. $x(1 - 2x)(2x + 1)$
D. $x(1 - 4x^{2})$
A. $x(1 - 2x)^{2}$
B. $x(2x - 1)(2x + 1)$
C. $x(1 - 2x)(2x + 1)$
D. $x(1 - 4x^{2})$
答案:
C
4. 如图,通过计算大正方形的面积,可以验证一个等式,这个等式是()
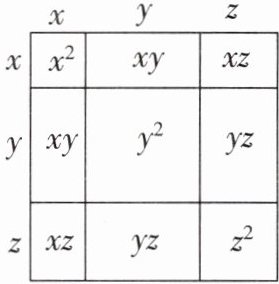
A. $(x + y + z)^{2}= x^{2}+y^{2}+z^{2}+2y + xz + yz$
B. $(x + y + z)^{2}= x^{2}+y^{2}+z + 2xy + xz + 2yz$
C. $(x + y + z)^{2}= x^{2}+y^{2}+z^{2}+2xy + 2xz + 2yz$
D. $(x + y + z)^{2}= (x + y)^{2}+2xz + 2yz$

A. $(x + y + z)^{2}= x^{2}+y^{2}+z^{2}+2y + xz + yz$
B. $(x + y + z)^{2}= x^{2}+y^{2}+z + 2xy + xz + 2yz$
C. $(x + y + z)^{2}= x^{2}+y^{2}+z^{2}+2xy + 2xz + 2yz$
D. $(x + y + z)^{2}= (x + y)^{2}+2xz + 2yz$
答案:
C
5. 若分式$\frac{4x - 9}{(3x + 2)(x - 1)}= \frac{A}{3x + 2}-\frac{B}{x - 1}$($A,B$为常数),则$A,B$的值分别为()
A. $A = 4,B = -9$
B. $A = 7,B = 1$
C. $A = 1,B = 7$
D. $A = -35,B = 13$
A. $A = 4,B = -9$
B. $A = 7,B = 1$
C. $A = 1,B = 7$
D. $A = -35,B = 13$
答案:
B
6. 如图,$M,N,P,R$分别是数轴上四个整数所对应的点,其中有一点是原点,并且$MN = NP = PR = 1$.数$a对应的点在M与N$之间,数$b对应的点在P与R$之间,若$|a|+|b| = 3$,则原点是()

A. 点$M或点R$
B. 点$N或点P$
C. 点$M或点N$
D. 点$P或点R$

A. 点$M或点R$
B. 点$N或点P$
C. 点$M或点N$
D. 点$P或点R$
答案:
A
7. 如图,设$k= \frac{S_{甲阴影}}{S_{乙阴影}}$
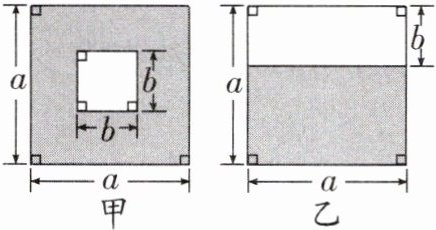
(a > b > 0),则有()
A. $k > 2$
B. $1 < k < 2$
C. $\frac{1}{2} < k < 1$
D. $0 < k < \frac{1}{2}$

(a > b > 0),则有()
A. $k > 2$
B. $1 < k < 2$
C. $\frac{1}{2} < k < 1$
D. $0 < k < \frac{1}{2}$
答案:
B
8. 已知$a_{1}$为实数,规定运算:$a_{2}= 1-\frac{1}{a_{1}},a_{3}= 1-\frac{1}{a_{2}},a_{4}= 1-\frac{1}{a_{3}},a_{5}= 1-\frac{1}{a_{4}},…,a_{n}= 1-\frac{1}{a_{n - 1}}$,按上述方法,当$a_{1}= 3$时,$\sqrt[3]{2a_{2025}}$的值等于()
A. $\frac{2}{3}$
B. $-\frac{1}{2}$
C. -1
D. 0
A. $\frac{2}{3}$
B. $-\frac{1}{2}$
C. -1
D. 0
答案:
C
查看更多完整答案,请扫码查看


