《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

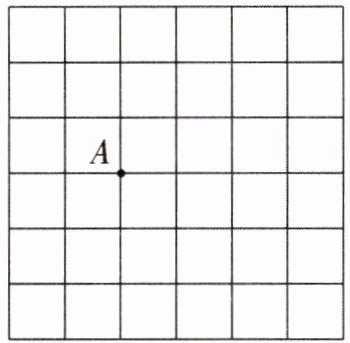
16. 如图,在$6×6$的网格中,每个小正方形的边长为 1,点 A 在格点(小正方形的顶点)上.试在各网格中画出顶点在格点上,面积为 6,且符合相应条件的图形.

答案：
符合条件的图形如图所示(答案不唯一):
　　 　　
图①:以点A为顶点的三角形　　图②:以点A为顶点的平行四边形　　图③:以点A为对角线交点的平行四边形

17. 如图,在$△ABC$中,$AB= AC$,D 是 BA 延长线上的一点,点 E 是 AC 的中点.
(1)实践与操作：利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).
①作$∠DAC$的平分线 AM；
②连结 BE 并延长交 AM 于点 F.
(2)猜想与证明：试猜想 AF 与 BC 有怎样的位置关系和数量关系,并说明理由.

答案：

(1)如图所示.
(2)$AF// BC$,且$AF=BC$.
理由如下:
$\because AB=AC$,
$\therefore ∠ABC=∠C$,
$\therefore ∠DAC=∠ABC+∠C=2∠C$.
由作图可得$∠DAC=2∠FAC$,
$\therefore ∠C=∠FAC$,
$\therefore AF// BC$.
$\because E$为$AC$的中点,
$\therefore AE=EC$;
在$△AEF$和$△CEB$中,
$\begin{cases}∠FAE = ∠C\\AE = CE\\∠AEF = ∠CEB\end{cases}$
$\therefore △AEF\cong △CEB(ASA),\therefore AF=CB$.