《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

21. (10分)如图①,将一张矩形纸片沿对角线剪开,得到两张三角形纸片,如图②,再将这两张三角形纸片摆成如图③所示的形式,使点$B$,$F$,$C$,$D$在同一条直线上.
(1)求证：$AB⊥DE$；
(2)若$PB= BC$,请找出图中与此条件有关的一对全等三角形,并给予证明.

答案：
(1)由题意，得∠A + ∠B = 90°，∠A = ∠D，
∴∠D + ∠B = 90°，
∴∠BPD = 180° - ∠B - ∠D = 90°，
∴AB⊥DE.
(2)答案不唯一,如:△ABC≌△DBP.证明如下:
∵∠B = ∠B，∠A = ∠D，BC = BP，
∴△ABC≌△DBP.

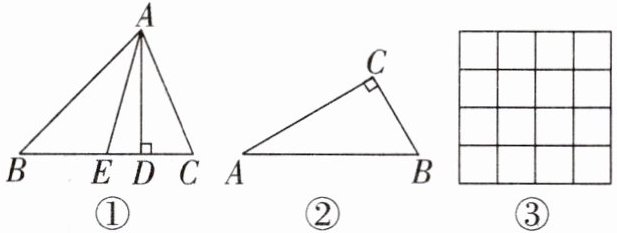
22. (10分)如图①,过$\triangle ABC的顶点A分别作对边BC上的高AD和中线AE$,点$D$是垂足,点$E是BC$的中点,规定$\lambda_{A}= \frac{DE}{BE}$.特别地,当点$D$,$E$重合时,规定$\lambda_{A}= 0$.另外,对$\lambda_{B}$,$\lambda_{C}$作类似的规定.
(1)如图②,已知$Rt\triangle ABC$中,$∠A= 30^{\circ}$,求$\lambda_{A}$,$\lambda_{C}$.
(2)如图③,在每个小正方形边长为1的$4×4$方格纸上,画一个$\triangle ABC$,使其顶点在格点(格点即每个小正方形的顶点)上,且$\lambda_{A}= 2$,面积也为2.
(3)判断下列命题的真假.(真命题打“√”,假命题打“×”)
①若$\triangle ABC中\lambda_{A}＜1$,则$\triangle ABC$为锐角三角形.()
②若$\triangle ABC中\lambda_{A}= 1$,则$\triangle ABC$为直角三角形.()
③若$\triangle ABC中\lambda_{A}＞1$,则$\triangle ABC$为钝角三角形.()

答案：

(1)如图，作CE⊥AB，垂足为E，作中线CF，AD.
∵AC⊥BC，
　
∴λ_A = $\frac{CD}{BD}$ = 1.
∵在Rt△ABC中，
　　∠CAB = 30°，
∴∠B = 60°.
　　又CF是△ABC的中线，
∴AF = CF = BF，
　
∴△CBF是正三角形.
　
∵CE⊥AB，
∴BF = 2EF，
∴λ_C = $\frac{EF}{AF}$ = $\frac{EF}{BF}$ = $\frac{1}{2}$.
　　　　　　　　　　　　　　　
(2)答案不唯一,如图所示.
　　　　　　　　　
(3)① × 解析:还需考虑λ_B和λ_C的值.
　② √ ③ √