《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

9. 如图,体育课上老师测量跳远成绩是这样操作的：用一块直角三角板的一边附在踏跳板上,另一边与拉直的皮尺重合,并且使皮尺经过被测试同学的落点,这样做的理由是______。

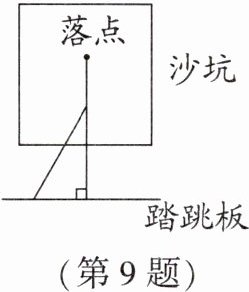
答案： 垂线段最短

10. 如图,与$∠1$是同位角的角是______,与$∠1$是内错角的角是______,与$∠1$是同旁内角的角是______。

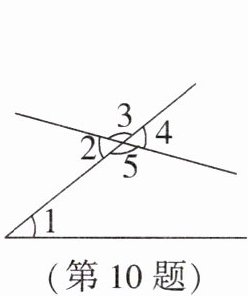
答案： ∠4　∠2　∠5

11. 把$15^{\circ }30'$化成度的形式,则$15^{\circ }30'= $______$^{\circ }$。

答案： 15.5

12. 从小岛O处同时开出三艘汽艇,A艇航向是南偏西$35^{\circ }$,B艇航向是东北方向,C艇航向为$∠AOB$(较小角)的平分线,则C艇的方向角是______。

答案： 南偏东50°

13. 如图,点O是直线AD上的点,$∠AOB,∠BOC,∠COD三个角从小到大依次相差25^{\circ }$,则这三个角的度数是______。

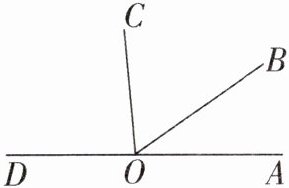
答案： 35°,60°,85°

14. 如图①是我们常用的折叠式小刀,图②中刀柄外形是一个直角梯形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图②所示的$∠1与∠2$,则$∠1与∠2$的度数和是______$^{\circ }$。

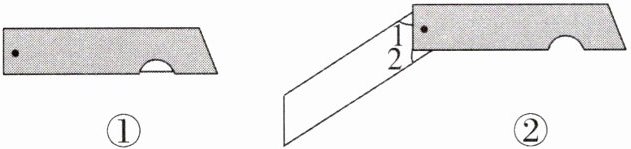
答案： 90

15. 如图,将$Rt△ABC$沿BC方向平移得到$Rt△DEF$,其中$AB= 8,BE= 10,DM= 4$,则阴影部分的面积是______。

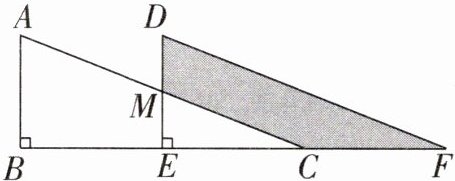
答案： 60

16. 瑞士著名数学家欧拉发现：简单多面体的顶点数V、面数F及棱数E之间满足一种有趣的关系：$V+F-E= 2$,这个关系式被称为欧拉公式。比如：正二十面体(如图),是由20个等边三角形所组成的正多面体,已知每个顶点处有5条棱,则可以通过欧拉公式算出正二十面体的顶点为______个。如果一个多面体的每个面都是五边形,每个顶点引出的棱都有3条,它是一个______面体。

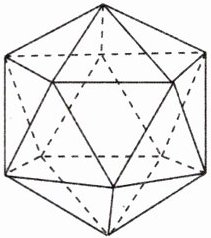
答案： 12 12

17. (6分)如图,O是直线AB上的一点,$∠COD$是直角,OE平分$∠BOC$。若$∠AOC= 30^{\circ }$,求$∠DOE$的度数。

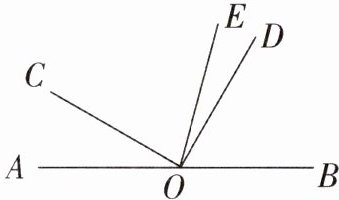
答案：
∵∠AOB=180°，∠COD=90°，
∴∠AOC+∠BOD=90°。
∵∠AOC=30°，
∴∠BOD=60°。
∵∠AOB=180°，∠AOC=30°，
∴∠BOC=150°。
∵OE平分∠BOC，
∴∠BOE=$\frac{1}{2}$∠BOC=75°，
∴∠DOE=∠BOE−∠DOB=75°−60°=15°。