第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
18. (6分)平面上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定蓄水池H的位置,使它与四个村庄(A,B,C,D四个村庄的地理位置如图所示)的距离之和
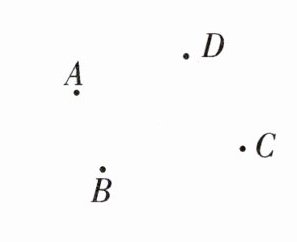
最小,并说明理由。
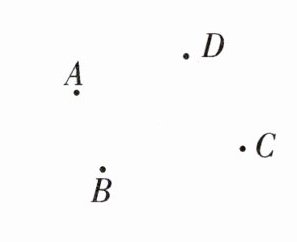
最小,并说明理由。
答案:
如图,连结AC,BD,它们的交点是H,点H就是蓄水池的位置,它到A,B,C,D的距离之和最小。

因为点H既在线段AC上,又在线段BD上,由两点之间线段最短,可知点H到A,B,C,D的距离之和最小。
如图,连结AC,BD,它们的交点是H,点H就是蓄水池的位置,它到A,B,C,D的距离之和最小。

因为点H既在线段AC上,又在线段BD上,由两点之间线段最短,可知点H到A,B,C,D的距离之和最小。
19. (6分)如图,在长为50m、宽为30m的长方形地块上,有纵横交错的几条小路,宽均为1m,其他部分均种植花草。试求出种植花草的面积是多少。
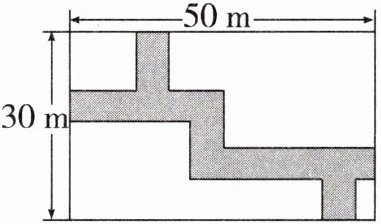

答案:
种植花草的面积S=(50−1)(30−1)=1421(m²)。
20. (8分)如图,$∠1= ∠2,∠BAE= ∠BDE$,EA平分$∠BEF$。
(1)求证:$AB// DE$。
(2)BD平分$∠EBC$吗?为什么?
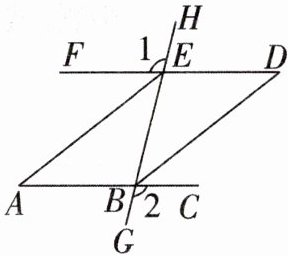
(1)求证:$AB// DE$。
(2)BD平分$∠EBC$吗?为什么?

答案:
(1)
∵∠2与∠ABE是对顶角,
∴∠2=∠ABE。
∵∠1=∠2,
∴∠1=∠ABE,
∴AB//DE。
(2)BD平分∠EBC。理由:
∵由
(1)知AB//DE,
∴∠BDE=∠DBC,∠BEF=∠EBC。
∵∠BAE=∠BDE,
∴∠BAE=∠DBC,
∴AE//BD,
∴∠AEB=∠DBE。
∵EA平分∠BEF,∠BEF=∠EBC,
∴BD平分∠EBC。
(1)
∵∠2与∠ABE是对顶角,
∴∠2=∠ABE。
∵∠1=∠2,
∴∠1=∠ABE,
∴AB//DE。
(2)BD平分∠EBC。理由:
∵由
(1)知AB//DE,
∴∠BDE=∠DBC,∠BEF=∠EBC。
∵∠BAE=∠BDE,
∴∠BAE=∠DBC,
∴AE//BD,
∴∠AEB=∠DBE。
∵EA平分∠BEF,∠BEF=∠EBC,
∴BD平分∠EBC。
21. (8分)如图,点C在线段AB上,点M,N分别是AC,BC的中点。
(1)若$AC= 8cm,CB= 6cm$,求线段MN的长。
(2)若C为线段AB上任一点,满足$AC+CB= a$,其他条件不变,你能猜想MN的长度吗?写出你的结论并说明理由。
(3)若C为直线AB上线段AB之外的任一点,且$AC= m,CB= n$,则线段MN的长为______。
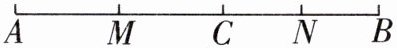
(1)若$AC= 8cm,CB= 6cm$,求线段MN的长。
(2)若C为线段AB上任一点,满足$AC+CB= a$,其他条件不变,你能猜想MN的长度吗?写出你的结论并说明理由。
(3)若C为直线AB上线段AB之外的任一点,且$AC= m,CB= n$,则线段MN的长为______。
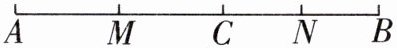
答案:
(1)MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$CB=4+3=7(cm)。
(2)MN=$\frac{1}{2}$a。理由如下:
MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$CB=$\frac{1}{2}$(AC+CB)=$\frac{1}{2}$a。
(3)$\frac{1}{2}$|m−n| 解析:当点C在线段AB的延长线上时,MN=$\frac{1}{2}$(m−n);当点C在线段BA的延长线上时,MN=$\frac{1}{2}$(n−m)。
综上可得MN=$\frac{1}{2}$|m−n|。
(1)MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$CB=4+3=7(cm)。
(2)MN=$\frac{1}{2}$a。理由如下:
MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$CB=$\frac{1}{2}$(AC+CB)=$\frac{1}{2}$a。
(3)$\frac{1}{2}$|m−n| 解析:当点C在线段AB的延长线上时,MN=$\frac{1}{2}$(m−n);当点C在线段BA的延长线上时,MN=$\frac{1}{2}$(n−m)。
综上可得MN=$\frac{1}{2}$|m−n|。
查看更多完整答案,请扫码查看


