《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

8. 如图,$△ABC$是正三角形,点 A 在第一象限,点$B(0,0)$、$C(1,0)$.将线段 CA 绕点 C 按顺时针方向旋转$120^{\circ }至CP_{1}$；将线段$BP_{1}$绕点 B 按顺时针方向旋转$120^{\circ }至BP_{2}$；将线段$AP_{2}$绕点 A 按顺时针方向旋转$120^{\circ }至AP_{3}$；将线段$CP_{3}$绕点 C 按顺时针方向旋转$120^{\circ }至CP_{4}$……以此类推,则点$P_{99}$的坐标是()

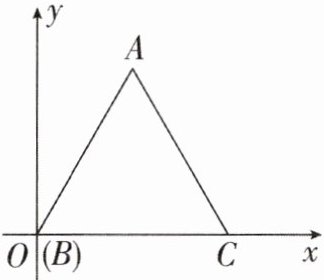
A. $(-49,100)$
B. $(-50,100)$
C. $(-49,50\sqrt {3})$
D. $(-50,50\sqrt {3})$

答案： C

9. 两个不相等的无理数,它们的乘积为有理数,这两个数可以是____.

答案： $\sqrt{2}$和$-\sqrt{2}$(答案不唯一)

10. 如图,点 E 是 AD 延长线上一点,如果添加一个条件,使$BC// AD$,则可添加的条件为____.(任意添加一个符合题意的条件即可)

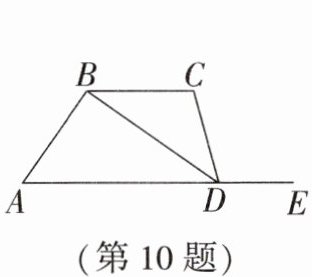
答案： $∠A+∠ABC=180^{\circ}$(答案不唯一)

11. 若一个一元二次方程的两个根分别是$Rt△ABC$的两条直角边长,且$S_{△ABC}= 3$,请写出一个符合题意的一元二次方程：____.

答案： $x^{2}-5x+6=0$(答案不唯一)

12. 如图,在平面直角坐标系中,点 A,B 的坐标分别为$(1,3),(n,3)$,若直线$y= 2x$与线段 AB 有公共点,则 n 的值可以为____.(写出一个即可)

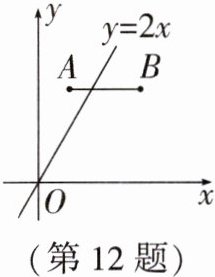
答案： 2(答案不唯一)

13. 如图,$∠ACD是△ABC$的外角,$∠ABC的平分线与∠ACD的平分线交于点A_{1},∠A_{1}BC的平分线与∠A_{1}CD的平分线交于点A_{2}... ... ∠A_{n-1}BC的平分线与∠A_{n-1}CD的平分线交于点A_{n}$.设$∠A= θ$,则：
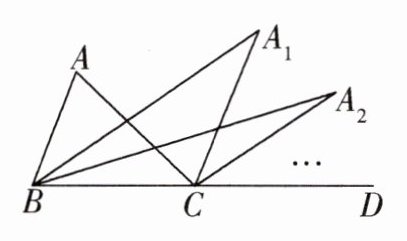
(1)$∠A_{1}= $____；
(2)$∠A_{n}= $____.

答案：
(1)$\frac {θ}{2}$　
(2)$\frac {θ}{2^{n}}$

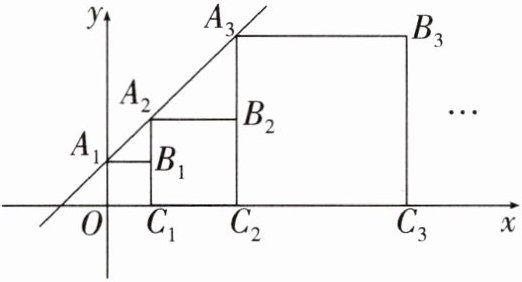
14. 正方形$A_{1}B_{1}C_{1}O,A_{2}B_{2}C_{2}C_{1},... $,按如图所示的方式放置.点$A_{1},A_{2},... 和点C_{1},C_{2},... 分别在直线y= x+1$和 x 轴上,则$A_{4}$的坐标是____；$B_{n}$的坐标是____.

答案： $(7,8)$　$(2^{n}-1,2^{n-1})$

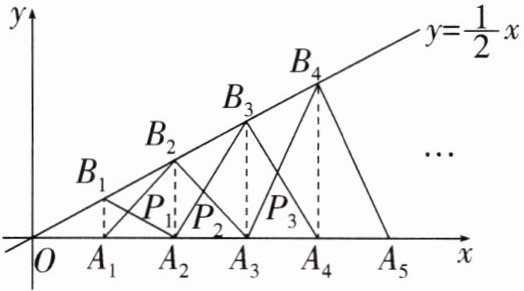
15. 如图,已知$A_{1},A_{2},A_{3},... ,A_{n}$是 x 轴上的点,且$OA_{1}= A_{1}A_{2}= A_{2}A_{3}= ... =A_{n}A_{n+1}= 1$,分别过点$A_{1},A_{2},A_{3},... ,A_{n+1}$作 x 轴的垂线交一次函数$y= \frac {1}{2}x的图象于点B_{1},B_{2},B_{3},... ,B_{n+1}$,连结$A_{1}B_{2},B_{1}A_{2},A_{2}B_{3},B_{2}A_{3},... ,A_{n}B_{n+1},B_{n}A_{n+1}依次产生交点P_{1},P_{2},P_{3},... ,P_{n}$,则$P_{n}$的横坐标是____.

答案： $n+\frac {n}{2n+1}$