《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

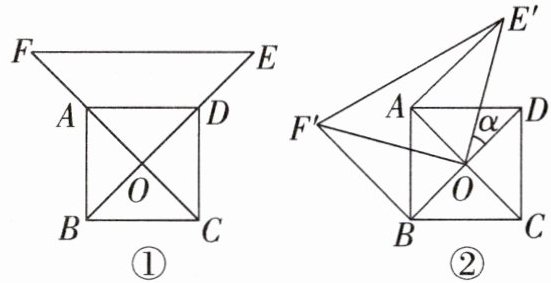
21. 如图①,$ O $ 为正方形 $ ABCD $ 的中心,分别延长 $ OA $ 到点 $ F $,$ OD $ 到点 $ E $,使 $ OF = 2OA $,$ OE = 2OD $,连结 $ EF $,将 $ \triangle FOE $ 绕点 $ O $ 按逆时针旋转 $ \alpha $ 角得到 $ \triangle F'OE' $(如图②).
(1) 探究 $ AE' $ 与 $ BF' $ 的数量关系,并给予证明；
(2) 当 $ \angle\alpha = 30^{\circ} $ 时,求证：$ \triangle AOE' $ 为直角三角形.

答案：

(1) $AE' = BF'$。证明如下:
　
∵ 在正方形 $ABCD$ 中，$AC \perp BD$，
　
∴ $\angle E'OF' = \angle AOD = \angle AOB = 90^{\circ}$，
　　　即 $\angle AOE' + \angle AOF' = \angle BOF' + \angle AOF'$，
　
∴ $\angle AOE' = \angle BOF'$。
　　　又 $OA = OB = OD$，$OE' = 2OD$，$OF' = 2OA$，
　
∴ $OE' = OF'$，
∴ $\triangle OAE' \cong \triangle OBF'$，
∴ $AE' = BF'$。
(2) 如图，作 $\triangle AOE'$ 的中线 $AM$，
　　　则 $OE' = 2OM = 2OD = 2OA$，
　
∴ $OA = OM$。
　
∵ $\angle \alpha = 30^{\circ}$，
∴ $\angle AOM = 60^{\circ}$，
　
∴ $\triangle AOM$ 为等边三角形，
　　　　　　　　　　　　　　　
∴ $MA = MO = ME'$，
　
∴ $\angle AE'M = \angle E'AM$。
　　　又 $\angle AE'M + \angle E'AM = \angle AMO$，
　　　即 $2\angle AE'M = 60^{\circ}$，
　
∴ $\angle AE'M = 30^{\circ}$，
∴ $\angle AE'M + \angle AOE' = 30^{\circ} + 60^{\circ} = 90^{\circ}$，
　
∴ $\triangle AOE'$ 为直角三角形。

22. 在平面直角坐标系 $ xOy $ 中,边长为 $ a $($ a $ 为大于 0 的常数)的正方形 $ ABCD $ 的对角线 $ AC,BD $ 相交于点 $ P $,顶点 $ A $ 在 $ x $ 轴正半轴上运动,顶点 $ B $ 在 $ y $ 轴正半轴上运动($ x $ 轴的正半轴、$ y $ 轴的正半轴都不包含原点 $ O $),顶点 $ C,D $ 都在第一象限.
(1) 当 $ \angle BAO = 45^{\circ} $ 时,求点 $ P $ 的坐标；
(2) 求证：无论点 $ A $ 在 $ x $ 轴正半轴上、点 $ B $ 在 $ y $ 轴正半轴上怎样运动,点 $ P $ 都在 $ \angle AOB $ 的平分线上；
(3) 设点 $ P $ 到 $ x $ 轴的距离为 $ h $,试确定 $ h $ 的取值范围,并说明理由.

答案：

(1) 当 $\angle BAO = 45^{\circ}$ 时，$\angle PAO = 90^{\circ}$。
在 $Rt\triangle AOB$ 中，$OA = \frac{\sqrt{2}}{2}AB = \frac{\sqrt{2}}{2}a$，
在 $Rt\triangle APB$ 中，$PA = \frac{\sqrt{2}}{2}AB = \frac{\sqrt{2}}{2}a$，
故点 $P$ 的坐标为 $(\frac{\sqrt{2}}{2}a, \frac{\sqrt{2}}{2}a)$。
(2) 如图，过点 $P$ 分别作 $x$ 轴、$y$ 轴的垂线，垂足分别为 $M$，$N$，
则有 $\angle PMA = \angle PNB = \angle NPM = \angle BPA = 90^{\circ}$，
　　　　　　　　　　　　　　
∴ $\angle BPA - \angle BPM = \angle NPM - \angle BPM$，
即 $\angle MPA = \angle NPB$。
又 $PA = PB$，
∴ $\triangle PAM \cong \triangle PBN$，
∴ $PM = PN$，
∴ 无论点 $A$ 在 $x$ 轴正半轴上、点 $B$ 在 $y$ 轴正半轴上怎样运动，点 $P$ 都在 $\angle AOB$ 的平分线上。
(3) $\frac{a}{2} ＜ h \leq \frac{\sqrt{2}}{2}a$。理由如下:当点 $B$ 与点 $O$ 重合时，点 $P$ 到 $x$ 轴的距离为 $\frac{a}{2}$，然后顶点 $A$ 在 $x$ 轴正半轴上向左运动，顶点 $B$ 在 $y$ 轴正半轴上向上运动，在此过程中，点 $P$ 到 $x$ 轴的距离先逐渐增大，直到当 $\angle BAO = 45^{\circ}$ 时，$PA \perp x$ 轴，这时点 $P$ 到 $x$ 轴的距离最大为 $\frac{\sqrt{2}}{2}a$，然后点 $P$ 到 $x$ 轴的距离又逐渐减小，直到点 $A$ 与点 $O$ 重合时，点 $P$ 到 $x$ 轴的距离为 $\frac{a}{2}$。
∵ $x$ 轴的正半轴、$y$ 轴的正半轴都不包含原点 $O$，
∴ 点 $P$ 到 $x$ 轴的距离 $h$ 的取值范围是 $\frac{a}{2} ＜ h \leq \frac{\sqrt{2}}{2}a$。