《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

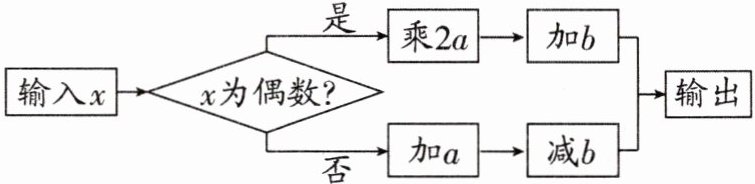
18. (8分)程序框图的算法思路源于我国古代数学名著《九章算术》,如图所示的程序框图,当输入$x$的值为4时,根据程序计算,输出的结果为5；当输入$x$的值为3时,根据程序计算,输出的结果为7,请你计算该程序框图中$a$,$b$的值。

答案： 根据题意，得$\begin{cases}4×2a + b = 5,\\3 + a - b = 7,\end{cases}$解得$\begin{cases}a = 1,\\b = -3,\end{cases}$
∴a，b的值分别为1，-3.

19. (8分)甲、乙两人解下面的方程组$\begin{cases}mx + 5y = 15, &①\\4x - ny = - 2. &②\end{cases}$由于甲看错了方程①中$m$的值,得到方程组的解为$\begin{cases}x = - 3,\\y = - 1,\end{cases}$乙看错了方程②中$n$的值,得到方程组的解为$\begin{cases}x = 5,\\y = 4.\end{cases}试求m^{2} + n^{2} + mn$的值。

答案： 根据题意，得$\begin{cases}4×(-3) - n×(-1) = -2,\\5m + 5×4 = 15,\end{cases}$解得$\begin{cases}m = -1,\\n = 10.\end{cases}$
∴$m^{2} + n^{2} + mn = 1 + 100 - 10 = 91$.

20. (8分)某班将举行“趣味数学知识竞赛”活动,班长安排小明购买奖品,下面是小明买回奖品时与班长的对话情况：
小明：买了两种不同的笔记本共40本,单价分别为5元和8元,我领了300元,现在找回68元。
班长：你肯定搞错了！
小明：哦！我把自己口袋里的13元一起当作找回的钱款了。
班长：这就对了！
请根据上面的信息,解决问题：
(1)试计算两种笔记本各买了多少本？
(2)请你解释：小明为什么不可能找回68元？

答案：
(1) 设5元的笔记本买了x本，8元的笔记本买了y本.
根据题意，得$\begin{cases}x + y = 40,\\5x + 8y + 68 = 300 + 13,\end{cases}$解得$\begin{cases}x = 25,\\y = 15.\end{cases}$
故5元的笔记本买了25本，8元的笔记本买了15本.
(2) 解法一：应找回钱款为$300 - 5×25 - 8×15 = 55$(元)，$55 ≠ 68$，故不可能找回68元.
解法二：设买m本5元的笔记本，则买$(40 - m)$本8元的笔记本.依题意，得$5m + 8(40 - m) = 300 - 68$，解得$m=\frac{88}{3}$.
∵m是正整数，
∴$m=\frac{88}{3}$不符合题意，舍去.
∴不可能找回68元.
解法三：买25本5元的笔记本和15本8元的笔记本的价钱总数应为奇数而不是偶数，故不可能找回68元