第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 在实数$\sqrt {2},π,-\frac {22}{7},\sqrt {16},3.14,3.1212212221...$(相邻两个1之间依次增加1个2)中,无理数有()
A. 2个
B. 3个
C. 4个
D. 5个
A. 2个
B. 3个
C. 4个
D. 5个
答案:
B
2. 实数$1 - 2a$有平方根,则$a$可以取的值为()
A. 0
B. 1
C. 2
D. 3
A. 0
B. 1
C. 2
D. 3
答案:
A
3. 下面计算正确的是()
A. $\pm \sqrt {(-3)^{2}} = 3$
B. $\sqrt {3} + \sqrt {2} = \sqrt {5}$
C. $\sqrt {27} ÷ \sqrt {3} = 3$
D. $\sqrt {4} = \pm 2$
A. $\pm \sqrt {(-3)^{2}} = 3$
B. $\sqrt {3} + \sqrt {2} = \sqrt {5}$
C. $\sqrt {27} ÷ \sqrt {3} = 3$
D. $\sqrt {4} = \pm 2$
答案:
C
4. 若$a = -\sqrt {25},b = \sqrt [3]{-1}$,则$a - b$的值为()
A. 4
B. -4
C. 6
D. -6
A. 4
B. -4
C. 6
D. -6
答案:
B
5. 设边长为3的正方形的对角线长为$a$。下列关于$a$的四种说法:①$a$是无理数;②$a$可以用数轴上的一个点来表示;③$3 < a < 4$;④$a$是18的算术平方根。其中,所有正确说法的序号是()
A. ①②③
B. ②③④
C. ①②④
D. ①③④
A. ①②③
B. ②③④
C. ①②④
D. ①③④
答案:
C
6. 如图,数轴上$A,B两点表示的数分别为-1和\sqrt {3}$,点$B关于点A的对称点为C$,则点$C$所表示的数为()
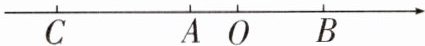
A. $-2 - \sqrt {3}$
B. $-1 - \sqrt {3}$
C. $-2 + \sqrt {3}$
D. $1 + \sqrt {3}$
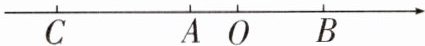
A. $-2 - \sqrt {3}$
B. $-1 - \sqrt {3}$
C. $-2 + \sqrt {3}$
D. $1 + \sqrt {3}$
答案:
A
7. 实数$a,b$在数轴上对应点的位置如图所示,则化简$\sqrt {a^{2}} + \sqrt {b^{2}} - \sqrt {(a - b)^{2}}$的结果是()
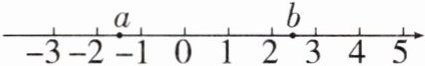
A. 0
B. $-2a$
C. $2b$
D. $-2a + 2b$
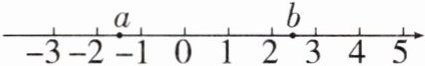
A. 0
B. $-2a$
C. $2b$
D. $-2a + 2b$
答案:
A
8. 已知在平面直角坐标系中,点$A的坐标是(\sqrt {2},-\sqrt {3})$,先将点$A$向右平移3个单位长度,然后再向上平移$3\sqrt {3}个单位长度后得到点B$,则点$B$的坐标是()
A. $(3\sqrt {2},3\sqrt {3})$
B. $(\sqrt {2} + 3,2\sqrt {3})$
C. $(\sqrt {2} - 3,-4\sqrt {3})$
D. $(3,3\sqrt {3})$
A. $(3\sqrt {2},3\sqrt {3})$
B. $(\sqrt {2} + 3,2\sqrt {3})$
C. $(\sqrt {2} - 3,-4\sqrt {3})$
D. $(3,3\sqrt {3})$
答案:
B
9. $\sqrt {81}$的平方根是____。
答案:
$\pm 3$
10. 化简:$(3 - 2\sqrt {2})^{2025} \cdot (3 + 2\sqrt {2})^{2024} = $____。
答案:
$3 - 2\sqrt{2}$
11. 比较大小:$\frac {\sqrt {5} - 1}{2}$____$0.5$。(填“>”“<”或“=”)
答案:
$>$
12. 使$\sqrt {12n}是整数的最小正整数n = $____。
答案:
3
13. 若$\sqrt [a - 1]{7}和\sqrt [3]{2b - 1}$都是7的立方根,则$a + b = $____。
答案:
8
14. 如图,半径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点$A$(滚动时与原点重合)由原点到达点$B$,则$AB$的长度就等于圆的周长,所以数轴上点$B$代表的数是____,它是一个____数。
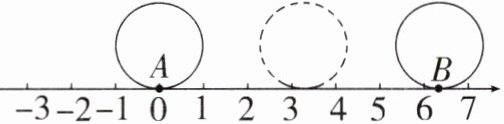

答案:
$2\pi$ 无理
15. 定义运算“@”的运算法则为$x@y = \sqrt {xy + 4}$,则$(2@6)@8 = $____。
答案:
6
17. (12分)计算:
(1)$(\sqrt [3]{-8})^{3} - \sqrt {(-8)^{2}} - (-\sqrt {4})^{2}$;
(2)$(5 + \sqrt {5})^{2} - (5 - \sqrt {5})^{2}$;
(3)$(\sqrt {3} + \sqrt {2})×(\sqrt {3} - \sqrt {2})×\sqrt {2} + (\sqrt {8})^{-1}$;
(4)$(3\sqrt {12} - 2\sqrt {\frac {1}{3}} + \sqrt {48}) ÷ 2\sqrt {3}$;
(5)$|-5| - \sqrt [3]{27} + (-2)^{2} + 4 ÷ (-\frac {2}{3})$;
(6)$20×\sqrt {\frac {4}{25}} - \sqrt [3]{-27} + 3 ÷ (-\frac {1}{3})$。
(1)$(\sqrt [3]{-8})^{3} - \sqrt {(-8)^{2}} - (-\sqrt {4})^{2}$;
(2)$(5 + \sqrt {5})^{2} - (5 - \sqrt {5})^{2}$;
(3)$(\sqrt {3} + \sqrt {2})×(\sqrt {3} - \sqrt {2})×\sqrt {2} + (\sqrt {8})^{-1}$;
(4)$(3\sqrt {12} - 2\sqrt {\frac {1}{3}} + \sqrt {48}) ÷ 2\sqrt {3}$;
(5)$|-5| - \sqrt [3]{27} + (-2)^{2} + 4 ÷ (-\frac {2}{3})$;
(6)$20×\sqrt {\frac {4}{25}} - \sqrt [3]{-27} + 3 ÷ (-\frac {1}{3})$。
答案:
(1)$-20$
(2)$20\sqrt{5}$
(3)$\frac{5\sqrt{2}}{4}$
(4)$\frac{14}{3}$
(5)0
(6)2
(1)$-20$
(2)$20\sqrt{5}$
(3)$\frac{5\sqrt{2}}{4}$
(4)$\frac{14}{3}$
(5)0
(6)2
查看更多完整答案,请扫码查看


