《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

1. 若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为()
A. 2cm
B. 4cm
C. 6cm
D. 8cm

答案： A

2. 已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为()
A. 50°
B. 80°
C. 50°或80°
D. 80°或65°

答案： C

3. 一直角三角形的两边长分别为3和4,则第三边的长为()
A. 5
B. $\sqrt{7}$
C. $\sqrt{5}$
D. 5或$\sqrt{7}$

答案： D

4. 如图,AD,CE分别是△ABC的中线和角平分线.若AB= AC,∠CAD= 20°,则∠ACE的度数是()

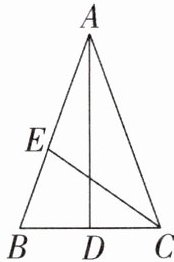
A. 20°
B. 35°
C. 40°
D. 70°

答案： B

5. 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为()

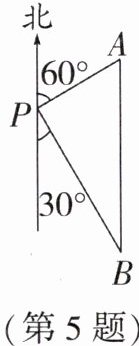
A. 60海里
B. 45海里
C. $20\sqrt{3}$海里
D. $30\sqrt{3}$海里

答案： D

6. 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A',使梯子的底端A'到墙根O的距离等于3m,同时梯子的顶端B下降至B',那么BB'()

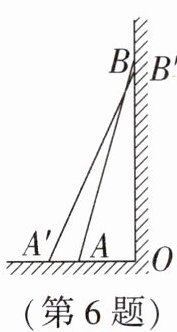
A. 小于1m
B. 大于1m
C. 等于1m
D. 小于或等于1m

答案： A

7. 如图,在△ABC中,∠C= 90°,DE垂直平分AB于点E,交AC于点D,AD= 2BC,则∠A等于()

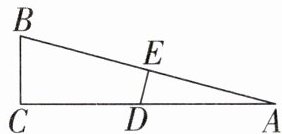
A. 15°
B. 25°
C. 30°
D. 35°

答案： A

8. 如图,已知$AB= A_1B,A_1B_1= A_1A_2,A_2B_2= A_2A_3,A_3B_3= A_3A_4,…,$若∠A= 70°,则$∠Aₙ₋_1AₙBₙ₋_1$的度数为()

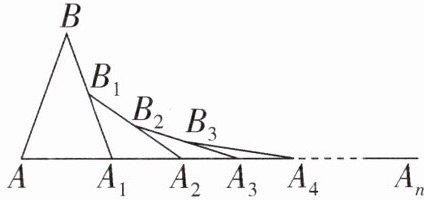
A. $\frac{70°}{2^n}$
B. $\frac{70°}{2^{n+1}}$
C. $\frac{70°}{2^{n-1}}$
D. $\frac{70°}{2^{n+2}}$

答案： C　解析:
∵在△ABA₁中,∠A = 70°,AB = A₁B,
∴∠BA₁A = 70°。
∵A₁A₂ = A₁B₁,∠BA₁A是△A₁A₂B₁的外角，
∴∠B₁A₂A₁ = $\frac{∠BA₁A}{2}$ = $\frac{70°}{2}$。同理可得∠B₂A₃A₂ = $\frac{∠B₁A₂A₁}{2}$ = $\frac{70°}{4}$，∠B₃A₄A₃ = $\frac{∠B₂A₃A₂}{2}$ = $\frac{70°}{8}$，
∴ ∠Aₙ₋₁AₙBₙ₋₁ = $\frac{70°}{2^{n - 1}}$。

9. 已知等腰三角形的底边长为6cm,一腰上的中线把这个三角形的周长分为两部分,这两部分的周长之差是3cm,那么这个等腰三角形的腰长是______.

答案： 9cm

22. (10分)(1)如图①,C点为线段AB上一点,△ACM,△CBN是等边三角形,AN与BM相等吗？说明理由.
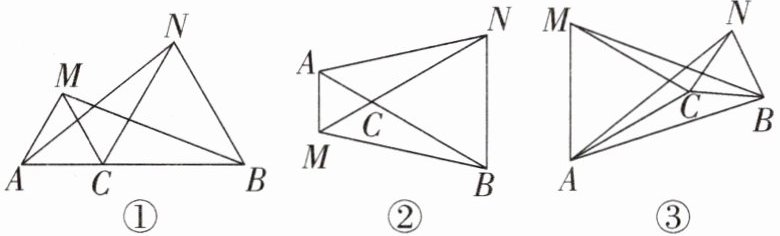
(2)如图②,C点为线段AB上一点,等边三角形ACM和等边三角形CBN在AB的异侧,此时AN与BM相等吗？说明理由.
(3)如图③,C点为线段AB外一点,△ACM,△CBN是等边三角形,AN与BM相等吗？说明理由.

答案：
(1)相等。理由如下:
　
∵△ACM,△CBN是等边三角形，
　
∴AC = CM,CN = BC,∠ACM = ∠BCN = 60°。
　　又∠ACN = ∠MCN + ∠ACM,∠MCB = ∠MCN + ∠BCN,
∴∠ACN = ∠MCB,
∴△ACN≌△MCB,
∴AN = BM。
(2)相等。理由如下:
　
∵△ACM,△CBN是等边三角形，
∴AC = CM,CN = BC。
　　又∠ACN = ∠MCB,
∴△ACN≌△MCB,
∴AN = BM。
(3)相等。理由如下:
　
∵△ACM,△CBN是等边三角形，
　
∴AC = CM,CN = BC,∠ACM = ∠BCN = 60°。
　　又∠ACN = ∠MCN + ∠ACM,∠MCB = ∠MCN + ∠BCN,
∴∠ACN = ∠MCB,
∴△ACN≌△MCB,
∴AN = BM。