《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

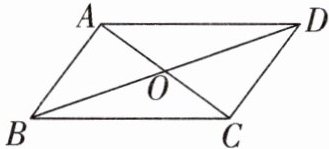
18. 如图,在四边形 ABCD 中,对角线 AC 与 BD 相交于点 O,在①$AB// CD$；②$AO= CO$；③$AD= BC$中任意选取两个作为条件,“四边形 ABCD 是平行四边形”作为结论构成命题.
(1)以①②作为条件构成的命题是真命题吗？若是,请证明；若不是,请举出反例.
(2)写出按题意构成的所有命题中的假命题,并举出反例加以说明.(命题请写成“如果……,那么……”的形式)

答案：

(1)是真命题.证明如下:
$\because AB// CD,\therefore ∠ABO=∠CDO$.
又$∠AOB=∠COD,AO=CO$,
$\therefore △ABO\cong △CDO(AAS)$,
$\therefore AB=CD$，$\therefore$四边形$ABCD$是平行四边形.
(2)假命题:①在四边形$ABCD$中,如果$AB// CD$,$AD=BC$,那么四边形$ABCD$是平行四边形;②在四边形$ABCD$中,对角线$AC$与$BD$相交于点$O$,如果$AO=CO,AD=BC$,那么四边形$ABCD$是平行四边形.
反例:如图①,在四边形$ABCD$中,$AB// CD,AD=BC$,但四边形$ABCD$不是平行四边形;如图②,在四边形$ABCD$中,$AO=CO,AD=BC$,但四边形$ABCD$不是平行四边形.

19. 某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程：
●操作发现：
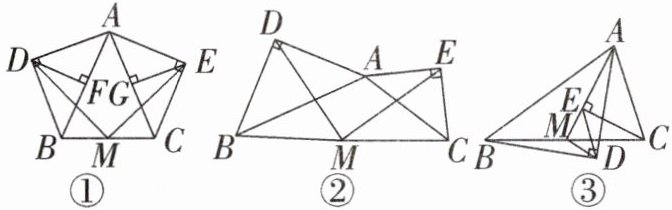
在等腰$△ABC$中,$AB= AC$,分别以 AB 和 AC 为斜边,向$△ABC$的外侧作等腰直角三角形,如图①所示,其中$DF⊥AB$于点 F,$EG⊥AC$于点 G,M 是 BC 的中点,连结 MD 和 ME,则下列结论正确的是____.(填序号)
①$AF= AG= \frac {1}{2}AB$；②$MD= ME$；③整个图形是轴对称图形；④$∠DAB= ∠DMB$.
●数学思考：
在任意$△ABC$中,分别以 AB 和 AC 为斜边,向$△ABC$的外侧作等腰直角三角形,如图②所示,M 是 BC 的中点,连结 MD 和 ME,则 MD 和 ME 具有怎样的数量和位置关系？请给出证明过程.
●类比探究：
在任意$△ABC$中,仍分别以 AB 和 AC 为斜边,向$△ABC$的内侧作等腰直角三角形,如图③所示,M 是 BC 的中点,连结 MD 和 ME,试判断$△MED$的形状.(不需要证明)

答案：
操作发现:①②③④
数学思考:$MD=ME,MD⊥ME$.证明如下:
如图,分别取$AB,AC$的中点$F,G$,连结$DF,MF$,$MG,EG$.
$\because M$是$BC$的中点,$\therefore MF// AC$,$MF=\frac {1}{2}AC$.
又$EG$是等腰$Rt△AEC$斜边上的中线,
$\therefore EG⊥AC$且$EG=\frac {1}{2}AC,\therefore MF=EG$.
同理可证$DF=MG$.
$\because MF// AC,\therefore ∠MFA+∠BAC=180^{\circ}$.
同理可得$∠MGA+∠BAC=180^{\circ},\therefore ∠MFA=∠MGA$.
又$EG⊥AC,\therefore ∠EGA=90^{\circ}$.
同理可得$∠DFA=90^{\circ}$,
$\therefore ∠MFA+∠DFA=∠MGA+∠EGA$,
即$∠DFM=∠MGE$.
又$MF=EG,DF=MG,\therefore △DFM\cong △MGE(SAS)$.
$\therefore MD=ME,∠DMF=∠MEG$;
而$∠DMF+∠FMB+∠DME+∠EMG+∠GMC=180^{\circ}$.
$\because MF// AC,\therefore ∠FMB=∠GCM$.
又$∠GCM+∠GMC+∠EMG+∠MEG=180^{\circ}-∠AGE=90^{\circ}$,
$\therefore ∠DME=90^{\circ}$,即$MD⊥ME$.
类比探究:$△MED$是等腰直角三角形.