《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

21. 共享电动车是一种新理念下的交通工具,扫码开锁,循环共享。某天早上王老师想骑共享电动车去学校,有$A$,$B$两种品牌的共享电动车可选择。已知,$A$品牌电动车骑行按时间收费；$B品牌电动车前10\mathrm{min}收费6$元,之后按超时时长收费,$A$,$B两种品牌电动车所收费用y_{A}$,$y_{B}与骑行时间x$之间的函数图象如图所示。

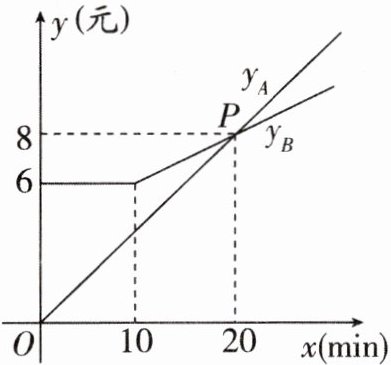
(1)写出$y_{A}$,$y_{B}关于x$的函数关系式,并说明图中函数$y_{A}与y_{B}图象的交点P$表示的实际意义。
(2)已知王老师家与学校的距离为$9\mathrm{km}$,且王老师骑电动车的平均速度为$300\mathrm{m/min}$,那么王老师选择哪种品牌的共享电动车会更省钱？请说明理由。
(3)当$x$为何值时,两种品牌共享电动车收费相差$3$元？

答案：
(1)用待定系数法代入图中点的坐标，可得$y_{A} = \frac{2}{5}x$，
$y_{B} = \begin{cases}6(0 ＜ x \leq 10)\\\frac{1}{5}x + 4(x ＞ 10)\end{cases}$。
因为点P的坐标为(20,8)，所以交点P表示的实际意义是当骑行时间为20min时，A、B两种品牌的共享电动车收费都为8元。
(2)选择B品牌共享电动车会更省钱。理由如下：
因为王老师家与学校的距离为9km，且王老师骑电动车的平均速度为300m/min，
所以王老师从家骑行到学校所需时间为$\frac{9000}{300} = 30(min)$，
观察函数图象可知，当x = 30时，$y_{A} ＞ y_{B}$，
所以选择B品牌共享电动车会更省钱。
(3)当0＜x≤10时，令$y_{B} - y_{A} = 3$，即$6 - \frac{2}{5}x = 3$，解得x = 7.5，符合题设；
当10＜x≤20时，令$y_{B} - y_{A} = 3$，即$\frac{1}{5}x + 4 - \frac{2}{5}x = 3$，解得x = 5，不符合题设，舍去；
当x＞20时，令$y_{A} - y_{B} = 3$，即$\frac{2}{5}x - (\frac{1}{5}x + 4) = 3$，解得x = 35，符合题设。
综上，当x为7.5或35时，两种品牌共享电动车收费相差3元。

22. 在矩形$ABCD$中,$AB = 4\mathrm{cm}$,$BC = 8\mathrm{cm}$,$AC的垂直平分线EF分别交AD$,$BC于点E$,$F$,垂足为$O$。
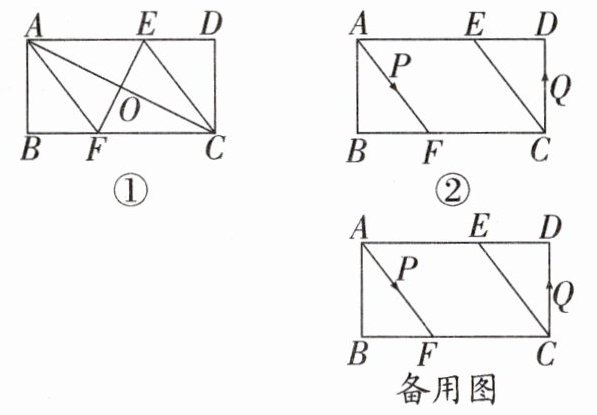
(1)如图①,连结$AF$,$CE$,求证：四边形$AFCE$为菱形,并求$AF$的长。
(2)如图②,动点$P$,$Q分别从A$,$C$两点同时出发,沿$\triangle AFB和\triangle CDE$各边匀速运动一周。即点$P自A\to F\to B\to A$停止,点$Q自C\to D\to E\to C$停止。在运动过程中：
①已知点$P的速度为5\mathrm{cm/s}$,点$Q的速度为4\mathrm{cm/s}$,运动时间为$t\mathrm{s}$,当以$A$,$C$,$P$,$Q$四点为顶点的四边形是平行四边形时,求$t$的值；
②若点$P$,$Q的运动路程分别为a$,$b$(单位：$\mathrm{cm}$,$ab\neq0$),已知以$A$,$C$,$P$,$Q$四点为顶点的四边形是平行四边形,求$a与b$满足的数量关系式。

答案：

(1)
∵四边形ABCD是矩形，
∴AD//BC。
∴∠CAD = ∠ACB，∠AEF = ∠CFE。
∵EF垂直平分AC，垂足为O，
∴OA = OC，
∴△AOE≌△COF，
∴OE = OF，
∴四边形AFCE为平行四边形。
又EF⊥AC，
∴平行四边形AFCE为菱形。
设菱形AFCE的边长为xcm，
则AF = CF = xcm，BF = (8 - x)cm，
在Rt△ABF中，AB = 4cm，
由勾股定理得$4^{2} + (8 - x)^{2} = x^{2}$，解得x = 5，
∴AF = 5cm。
(2)①显然当P点在AF上，Q点在CD上时，A，C，P，Q四点不可能构成平行四边形；同理P点在AB上，Q点在DE或CE上时，也不能构成平行四边形；P点在BF上，Q点在CD上时，也不能构成平行四边形。因此只有当P点在BF上，Q点在ED上时，才能构成平行四边形（如图①所示），
∴以A，C，P，Q四点为顶点的四边形是平行四边形时，PC = QA。
∵点P的速度为5cm/s，点Q的速度为4cm/s，运动时间为ts，
∴PC = 5tcm，QA = (12 - 4t)cm，
∴5t = 12 - 4t，解得$t = \frac{4}{3}$，

∴以A，C，P，Q四点为顶点的四边形是平行四边形时，$t = \frac{4}{3}$。
②由题意得，以A，C，P，Q四点为顶点的四边形是平行四边形时，点P，Q在互相平行的对应边上。分三种情况：
(i)如图②，当点P在AF上，点Q在CE上时，AP = CQ，即a = 12 - b，得a + b = 12；
(ii)如图③，当点P在BF上，点Q在DE上时，AQ = CP，即12 - b = a，得a + b = 12；
(iii)如图④，当点P在AB上，点Q在CD上时，AP = CQ，即12 - a = b，得a + b = 12。
综上所述，a与b满足的数量关系式是$a + b = 12(ab \neq 0)$。