《2025年暑假总动员宁夏人民教育出版社八升九数学浙教版》

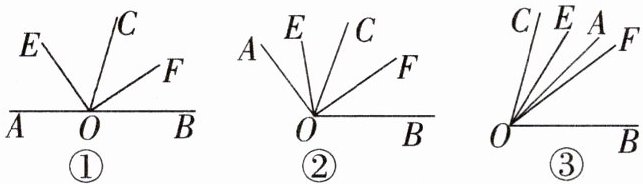
22. (8分)下列各小题中,都有OE平分$∠AOC$,OF平分$∠BOC$。
(1)如图①,若点A,O,B在一条直线上,则$∠AOB与∠EOF$的数量关系是什么？
(2)如图②,若点A,O,B不在一条直线上,则(1)中的数量关系是否成立？请说明理由。
(3)如图③,若OA在$∠BOC$的内部,则(1)中的数量关系是否成立？请说明理由。

答案：
(1)∠EOF=$\frac{1}{2}$∠AOB。
(2)成立。理由如下:
∵OE平分∠AOC，
∴∠EOC=$\frac{1}{2}$∠AOC。
∵OF平分∠BOC，
∴∠COF=$\frac{1}{2}$∠BOC。
∴∠EOF=∠EOC+∠COF=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$∠AOB。
(3)成立。理由如下:
∵OE平分∠AOC，
∴∠EOC=$\frac{1}{2}$∠AOC。
∵OF平分∠BOC，
∴∠COF=$\frac{1}{2}$∠BOC。
∴∠EOF=∠COF−∠EOC=$\frac{1}{2}$∠BOC−$\frac{1}{2}$∠AOC=$\frac{1}{2}$(∠BOC−∠AOC)=$\frac{1}{2}$∠AOB。

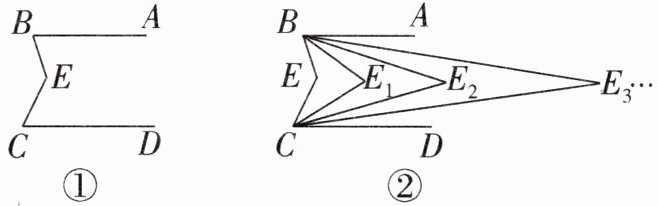
23. (10分)如图,已知$AB// CD$,CE,BE的交点为E,现作如下操作：
第一次操作,分别作$∠ABE和∠DCE$的平分线,交点为$E_{1}$；
第二次操作,分别作$∠ABE_{1}和∠DCE_{1}$的平分线,交点为$E_{2}$；
第三次操作,分别作$∠ABE_{2}和∠DCE_{2}$的平分线,交点为$E_{3}$；…；
第n次操作,分别作$∠ABE_{n-1}和∠DCE_{n-1}$的平分线,交点为$E_{n}$。
(1)如图①,求证：$∠BEC= ∠ABE+∠DCE$；
(2)如图②,求证：$∠BE_{2}C= \frac {1}{4}∠BEC$；
(3)猜想：若$∠E_{n}= α$度,那么$∠BEC$等于多少度？(直接写出结论)

答案：

(1)如图，过点E作EF//AB。
∵AB//CD，
∴AB//EF//CD，
∴∠B=∠1，∠C=∠2。
　　　　　　　　　　　　　　　　
∵∠BEC=∠1+∠2，
∴∠BEC=∠ABE+∠DCE。
(2)
∵∠ABE和∠DCE的平分线交点为E₁，
∴由
(1)可得，∠CE₁B=∠ABE₁+∠DCE₁=$\frac{1}{2}$∠ABE+$\frac{1}{2}$∠DCE=$\frac{1}{2}$∠BEC。
∵∠ABE₁和∠DCE₁的平分线交点为E₂，
∴由
(1)可得，∠BE₂C=∠ABE₂+∠DCE₂=$\frac{1}{2}$∠ABE₁+$\frac{1}{2}$∠DCE₁=$\frac{1}{2}$∠CE₁B=$\frac{1}{4}$∠BEC。
(3)当∠Eₙ=α度时，∠BEC=2ⁿα度。