《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

阅读教材 $P_{37}\sim P_{39}$ 内容,归纳结论：
1. 相似三角形对应____的比,对应____的比与对应____的比都等于相似比.
一般地,相似三角形对应线段的比等于相似比.
2. 相似三角形周长的比等于____.
3. 相似三角形面积的比等于____.

答案： 1. 高 中线 角平分线
2. 相似比
3. 相似比的平方

1. 已知两个相似三角形的相似比是 $\frac{2}{3}$,则下列关于这两个相似三角形的判断中,错误的是()
A. 对应边的比为 $\frac{2}{3}$
B. 对应中线的比为 $\frac{2}{3}$
C. 对应角的比为 $\frac{2}{3}$
D. 对应高的比为 $\frac{2}{3}$

答案： C

2. 已知 $\triangle ABC\backsim\triangle DEF$,且 $\frac{AB}{DE}= \frac{1}{3}$,若 $\triangle ABC$ 的周长为 2,则 $\triangle DEF$ 的周长为()
A. $\frac{2}{9}$
B. $\frac{2}{3}$
C. 6
D. 18

答案： C

3. 如图,在 $\triangle ABC$ 中,$D$,$E$ 分别是 $AB$ 和 $AC$ 边上的点,且 $\frac{AD}{AB}= \frac{AE}{AC}= \frac{2}{3}$.
(1) 若 $DE = 6$,求 $BC$ 的长；
(2) 若四边形 $BDEC$ 的面积为 10,求 $\triangle ADE$ 的面积.

答案：
(1) 9
(2) 8

4. 能力提升(教材 $P_{39}$ 练习 $T_{2}$)如图,$\triangle ABC$ 与 $\triangle A'B'C'$ 相似,$AD$,$BE$ 是 $\triangle ABC$ 的高,$A'D'$,$B'E'$ 是 $\triangle A'B'C'$ 的高,求证：$\frac{AD}{A'D'}= \frac{BE}{B'E'}$.

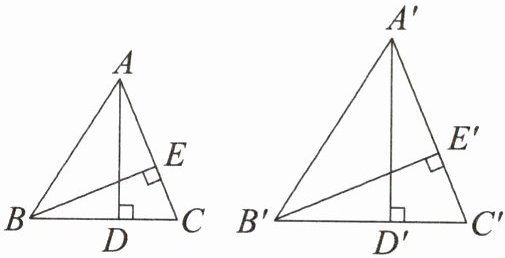
答案： 【解析】：
因为$\triangle ABC$与$\triangle A'B'C'$相似，所以$\angle ABC = \angle A'B'C'$，$\angle BAC=\angle B'A'C'$。
又因为$AD$，$BE$是$\triangle ABC$的高，$A'D'$，$B'E'$是$\triangle A'B'C'$的高，所以$\angle ADB=\angle A'D'B' = 90^{\circ}$，$\angle BEA=\angle B'E'A' = 90^{\circ}$。
在$\triangle ABD$和$\triangle A'B'D'$中，$\angle ABD=\angle A'B'D'$，$\angle ADB=\angle A'D'B'$，根据两角分别相等的两个三角形相似，可得$\triangle ABD\sim\triangle A'B'D'$，则$\frac{AD}{A'D'}=\frac{AB}{A'B'}$。
在$\triangle ABE$和$\triangle A'B'E'$中，$\angle BAE=\angle B'A'E'$，$\angle BEA=\angle B'E'A'$，根据两角分别相等的两个三角形相似，可得$\triangle ABE\sim\triangle A'B'E'$，则$\frac{BE}{B'E'}=\frac{AB}{A'B'}$。
所以$\frac{AD}{A'D'}=\frac{BE}{B'E'}$。
【答案】：$\frac{AD}{A'D'}=\frac{BE}{B'E'}$