知识梳理
k的几何意义(拓展):在反比例函数$y= \frac {k}{x}$的图象上,任取一点向坐标轴作垂线,以这一点、垂足和坐标原点为顶点的三角形的面积$S= $____.
k的几何意义(拓展):在反比例函数$y= \frac {k}{x}$的图象上,任取一点向坐标轴作垂线,以这一点、垂足和坐标原点为顶点的三角形的面积$S= $____.
答案:
$\frac { | k | } { 2 }$
1. 如图,点A在反比例函数$y= \frac {k}{x}(x<0)$的图象上,$AB⊥x$轴于点B,若$\triangle AOB$的面积为2,则k的值为 ()
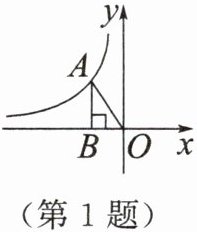
A. -4
B. 4
C. -2
D. 2

A. -4
B. 4
C. -2
D. 2
答案:
A
2. (教材$P_{7}$例4变式)已知反比例函数$y= \frac {a-\sqrt {2}}{x}$的图象的一支位于第二象限.
(1)图象的另一支位于第____象限,常数a的取值范围是____;
(2)在这个函数图象的某一支上任取点$A(x_{1},y_{1})和B(x_{2},y_{2})$,如果$x_{1}>x_{2}$,那么$y_{1}与y_{2}的大小关系为y_{1}$____$y_{2}$.
(1)图象的另一支位于第____象限,常数a的取值范围是____;
(2)在这个函数图象的某一支上任取点$A(x_{1},y_{1})和B(x_{2},y_{2})$,如果$x_{1}>x_{2}$,那么$y_{1}与y_{2}的大小关系为y_{1}$____$y_{2}$.
答案:
(1)四 $ a < \sqrt { 2 } $
(2) >
(1)四 $ a < \sqrt { 2 } $
(2) >
3. (教材$P_{8}练习T_{1}$)已知一个反比例函数的图象经过点$A(3,-4).$
(1)这个函数的图象位于哪些象限?在图象的每一支上,y随x的增大如何变化?
(2)点$B(-3,4),C(-2,6),D(3,4)$是否在这个函数的图象上?为什么?
(1)这个函数的图象位于哪些象限?在图象的每一支上,y随x的增大如何变化?
(2)点$B(-3,4),C(-2,6),D(3,4)$是否在这个函数的图象上?为什么?
答案:
(1)略
(2)点 B、点 C 在这个函数的图象上,点 D 不在这个函数的图象上,理由略
(1)略
(2)点 B、点 C 在这个函数的图象上,点 D 不在这个函数的图象上,理由略
4. 能力提升如图,一次函数$y= kx+b$(k,b为常数,$k≠0$)的图象与反比例函数$y= \frac {m}{x}$(m为常数,$m≠0$)的图象相交于$A(2,a),B(-1,2)$两点.
(1)求一次函数的解析式;
(2)根据图象,请直接写出关于x的不等式$kx+b>\frac {m}{x}$的解集.
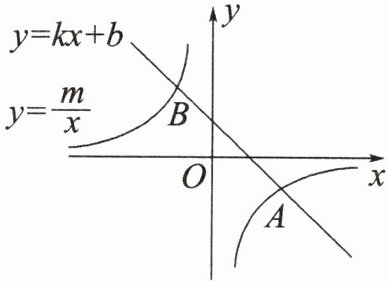
(1)求一次函数的解析式;
(2)根据图象,请直接写出关于x的不等式$kx+b>\frac {m}{x}$的解集.

答案:
(1) $ y = - x + 1 $
(2) $ x < - 1 $ 或 $ 0 < x < 2 $
(1) $ y = - x + 1 $
(2) $ x < - 1 $ 或 $ 0 < x < 2 $
查看更多完整答案,请扫码查看


