《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

阅读教材$P_{85}\sim P_{87}$内容,归纳结论:
1. 圆周角定义:顶点在圆上,并且两边都与圆____的角叫做圆周角.
2. 圆周角定理:一条弧所对的圆周角等于它所对的圆心角的____.
3. 推论:同弧或等弧所对的圆周角____.半圆(或直径)所对的圆周角是____,$90^{\circ }$的圆周角所对的弦是____.

答案： 1. 相交
2. 一半
3. 相等 直角 直径

1. 如图,点A,B,C在$\odot O$上,若$∠BAC= 30^{\circ }$,则$∠BOC$的度数是 ()

A.$30^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$75^{\circ }$

答案： C

2. 如图,AB是$\odot O$的直径,若AB的长为8 cm,点D在圆上,且$∠ADC= 30^{\circ }$,则弦AC的长为____cm.

答案： 4

3. (教材$P_{90}T_{14}$)如图,A,P,B,C是$\odot O$上的四个点,$∠APC= ∠CPB= 60^{\circ }$.判断$\triangle ABC$的形状,并证明你的结论.

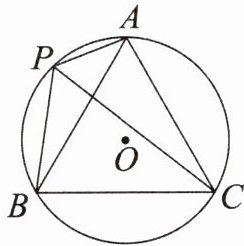
答案： △ABC 是等边三角形，证明略

4. 能力提升如图,已知AB是$\odot O$的直径,C是$\odot O$上一点,连接BC,AC,D是$\overset{\frown }{AC}$的中点,连接OD交AC于点E.
(1)求证:$OD// BC$.
(2)若$AC= 8,DE= 2$,求BC的长.

答案：
(1)略
(2)6