阅读教材$P_{97}\sim P_{98}$内容,归纳结论:
1. 切线的判定定理:经过____的外端并且____这条____的直线是圆的切线.
2. 切线的性质定理:圆的切线____过切点的半径.
3. 证明切线的方法:①切线的判定定理;②圆心到直线的距离等于____.
1. 切线的判定定理:经过____的外端并且____这条____的直线是圆的切线.
2. 切线的性质定理:圆的切线____过切点的半径.
3. 证明切线的方法:①切线的判定定理;②圆心到直线的距离等于____.
答案:
1. 半径 垂直于 半径 2. 垂直于 3. 半径
1. 如图,$PA为\odot O$的切线,$A$为切点,$OP交\odot O于点B$,连接$AB$.若$∠PAB= 22^{\circ }$,则$∠AOB$的度数为 ()
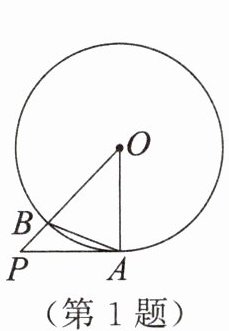
A.$22^{\circ }$
B.$40^{\circ }$
C.$44^{\circ }$
D.$68^{\circ }$

A.$22^{\circ }$
B.$40^{\circ }$
C.$44^{\circ }$
D.$68^{\circ }$
答案:
C
2. 如图,$AB是\odot O$的直径,点$D在\odot O$上,过点$D作\odot O的切线DC交AB的延长线于点C$.若$BC= 4,CD= 8$,则$\odot O$的半径为____.
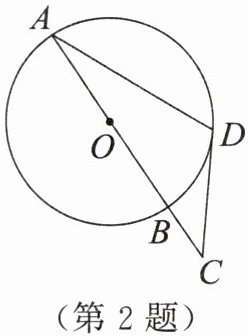

答案:
6
3. 如图,$AB是\odot O$的直径,$∠B= ∠CAD$. 求证:$AC是\odot O$的切线.
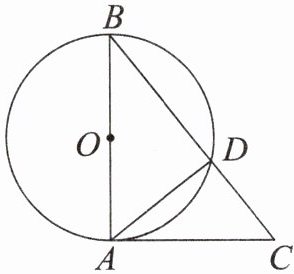

答案:
【解析】:
- 因为$AB$是$\odot O$的直径,根据直径所对的圆周角是直角,所以$\angle ADB = 90^{\circ}$。
- 在$\triangle ABD$中,$\angle BAD+\angle B = 90^{\circ}$(直角三角形两锐角互余)。
- 又因为$\angle B=\angle CAD$(已知条件),将$\angle B$替换为$\angle CAD$,则$\angle BAD+\angle CAD = 90^{\circ}$,即$\angle BAC = 90^{\circ}$。
- 根据切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线,$AB$是$\odot O$的半径,$AC\perp AB$,所以$AC$是$\odot O$的切线。
【答案】:
$\because AB$是$\odot O$直径,$\therefore\angle ADB = 90^{\circ}$,$\therefore\angle BAD+\angle B = 90^{\circ}$,$\because\angle B=\angle CAD$,$\therefore\angle BAD+\angle CAD = 90^{\circ}$,即$\angle BAC = 90^{\circ}$,$\therefore AB\perp AC$,又$\because AB$是$\odot O$半径,$\therefore AC$是$\odot O$的切线。
- 因为$AB$是$\odot O$的直径,根据直径所对的圆周角是直角,所以$\angle ADB = 90^{\circ}$。
- 在$\triangle ABD$中,$\angle BAD+\angle B = 90^{\circ}$(直角三角形两锐角互余)。
- 又因为$\angle B=\angle CAD$(已知条件),将$\angle B$替换为$\angle CAD$,则$\angle BAD+\angle CAD = 90^{\circ}$,即$\angle BAC = 90^{\circ}$。
- 根据切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线,$AB$是$\odot O$的半径,$AC\perp AB$,所以$AC$是$\odot O$的切线。
【答案】:
$\because AB$是$\odot O$直径,$\therefore\angle ADB = 90^{\circ}$,$\therefore\angle BAD+\angle B = 90^{\circ}$,$\because\angle B=\angle CAD$,$\therefore\angle BAD+\angle CAD = 90^{\circ}$,即$\angle BAC = 90^{\circ}$,$\therefore AB\perp AC$,又$\because AB$是$\odot O$半径,$\therefore AC$是$\odot O$的切线。
4. 能力提升如图,$AB是\odot O$的直径,$CD是\odot O$的切线,切点为$C$,$BE⊥CD$,垂足为$E$,连接$AC$,$BC$.
(1)求证:$BC平分∠ABE$.
(2)若$∠A= 60^{\circ },OA= 2$,求$CE$的长.
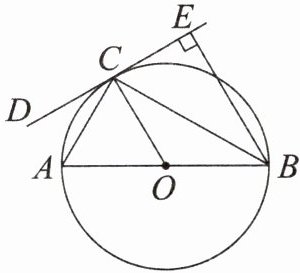
(1)求证:$BC平分∠ABE$.
(2)若$∠A= 60^{\circ },OA= 2$,求$CE$的长.

答案:
(1)略
(2)$\sqrt{3}$
(1)略
(2)$\sqrt{3}$
查看更多完整答案,请扫码查看


