《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

阅读教材 $ P_{92} \sim P_{95} $ 内容,归纳结论：
1. 设 $ \odot O $ 的半径为 $ r $,点 $ P $ 到圆心的距离 $ OP = d $,则有：
点 $ P $ 在圆外 $ \Leftrightarrow d $______ $ r $；点 $ P $ 在圆上 $ \Leftrightarrow d $______ $ r $；点 $ P $ 在圆内 $ \Leftrightarrow d $______ $ r $。
2. 不在同一条直线上的______个点确定一个圆。
3. 经过三角形的______可以作一个圆,这个圆叫做三角形的外接圆,外接圆的圆心是三角形三条边的______的交点,叫做这个三角形的外心。
4. 反证法：假设命题的结论______,由此经过推理得出______,由矛盾断定所作假设______,从而得到原命题成立。

答案： 1. $＞$ $=$ $＜$
2. 三
3. 三个顶点 垂直平分线
4. 不成立 矛盾 不正确

1. 已知 $ \odot O $ 的半径为 $ 8 \mathrm{cm} $,点 $ A $ 在 $ \odot O $ 外,则 $ OA $ 的长可能为()
A. $ 6 \mathrm{cm} $
B. $ 7 \mathrm{cm} $
C. $ 8 \mathrm{cm} $
D. $ 9 \mathrm{cm} $

答案： D

2. 已知 $ \odot O $ 的直径为 $ 4 $,点 $ P $ 与 $ \odot O $ 在同一平面内,$ PO = 2 $,则点 $ P $ 与 $ \odot O $ 的位置关系是()
A. 点 $ P $ 在 $ \odot O $ 内
B. 点 $ P $ 在 $ \odot O $ 上
C. 点 $ P $ 在 $ \odot O $ 外
D. 无法判断

答案： B

3. 牛顿曾说过：“反证法是数学家最精良的武器之一”。用反证法证明命题“一个三角形中不能有两个角是直角”时,应先假设()
A. 一个三角形中有两个角是直角
B. 一个三角形中有两个角是钝角
C. 一个三角形中有两个角是锐角
D. 一个三角形中有一个角是直角

答案： A

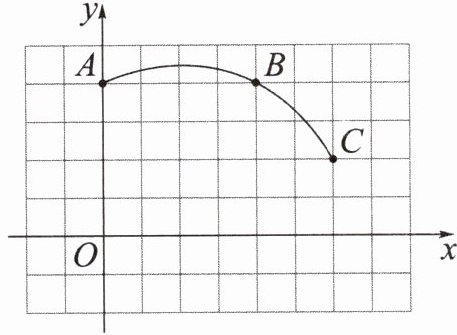
4. 如图,在正方形网格中,每个小正方形的边长都为 $ 1 $,一条圆弧经过格点 $ A $,$ B $,$ C $,现在以格点 $ O $ 为原点、竖直和水平方向为坐标轴建立平面直角坐标系。
(1) 请标出该圆弧所在圆的圆心 $ D $,并写出圆心 $ D $ 的坐标；
(2) 求 $ \odot D $ 的半径；
(3) 若点 $ E $ 的坐标是 $ (-1,3) $,试判断点 $ E $ 与 $ \odot D $ 的位置关系,并说明你的理由。

答案：
(1) 图略；$(2,0)$
(2)$2\sqrt{5}$
(3) 点$E$在$\odot D$内部，理由略

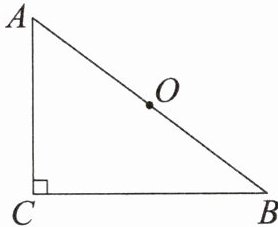
5. 如图,在 $ \mathrm{Rt} \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ AC = 6 $,$ BC = 8 $,点 $ O $ 是 $ AB $ 的中点。
(1) 若以点 $ O $ 为圆心,以 $ R $ 为半径作 $ \odot O $,且点 $ A $,$ B $,$ C $ 都在 $ \odot O $ 上,求 $ R $ 的值；
(2) 若以点 $ B $ 为圆心,以 $ r $ 为半径作 $ \odot B $,且点 $ O $,$ A $,$ C $ 中有两个点在 $ \odot B $ 内,有一个点在 $ \odot B $ 外,求 $ r $ 的取值范围。

答案：
(1) 5
(2)$8 ＜ r ＜ 10$