阅读教材$P_{29}\sim P_{32}$内容,归纳结论:
一般地,抛物线$y= ax^{2}$的对称轴是____,顶点坐标是____;当$a>0$时,抛物线开口向____,顶点是抛物线的最____点;当$a<0$时,抛物线开口向____,顶点是抛物线的最____点;对于抛物线$y= ax^{2}$,$|a|$越大,抛物线的开口越____。
一般地,抛物线$y= ax^{2}$的对称轴是____,顶点坐标是____;当$a>0$时,抛物线开口向____,顶点是抛物线的最____点;当$a<0$时,抛物线开口向____,顶点是抛物线的最____点;对于抛物线$y= ax^{2}$,$|a|$越大,抛物线的开口越____。
答案:
$y$轴 $(0,0)$ 上 低 下 高 小
1. 已知函数$y= -\frac {2}{3}x^{2}$,如图,在平面直角坐标系中画出图象,回答下列问题:
(1)图象开口向____,对称轴是____,顶点坐标是____;
(2)当$x= $____时,函数$y$有最____值,最大值为____;
(3)当$x$____时,$y随x$的增大而增大;
(4)若点$A(-3,y_{1})$,$B(3,y_{2})在函数y= -\frac {2}{3}x^{2}$的图象上,则$y_{1}$____$y_{2}$(填“>”“<”或“=”);
(5)若点$C(-6,y_{3})$,$D(4,y_{4})在函数y= -\frac {2}{3}x^{2}$的图象上,则$y_{3}$____$y_{4}$(填“>”“<”或“=”);
(6)若点$E(a^{2},y_{5})$,$F(a^{2}+1,y_{6})在函数y= -\frac {2}{3}x^{2}$的图象上,则$y_{5}$____$y_{6}$(填“>”“<”或“=”);
(7)与抛物线$y= -\frac {2}{3}x^{2}$开口大小相同,方向相反的抛物线为____。
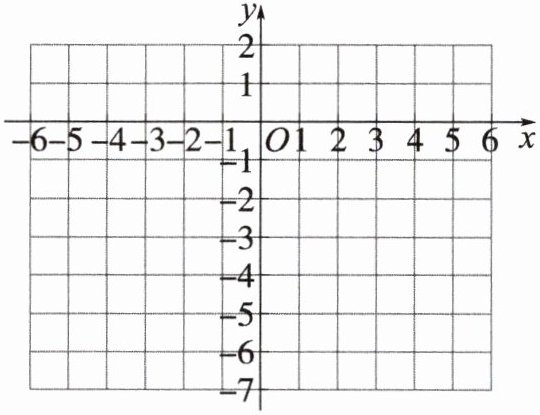
(1)图象开口向____,对称轴是____,顶点坐标是____;
(2)当$x= $____时,函数$y$有最____值,最大值为____;
(3)当$x$____时,$y随x$的增大而增大;
(4)若点$A(-3,y_{1})$,$B(3,y_{2})在函数y= -\frac {2}{3}x^{2}$的图象上,则$y_{1}$____$y_{2}$(填“>”“<”或“=”);
(5)若点$C(-6,y_{3})$,$D(4,y_{4})在函数y= -\frac {2}{3}x^{2}$的图象上,则$y_{3}$____$y_{4}$(填“>”“<”或“=”);
(6)若点$E(a^{2},y_{5})$,$F(a^{2}+1,y_{6})在函数y= -\frac {2}{3}x^{2}$的图象上,则$y_{5}$____$y_{6}$(填“>”“<”或“=”);
(7)与抛物线$y= -\frac {2}{3}x^{2}$开口大小相同,方向相反的抛物线为____。

答案:
图略
(1)下 $y$ 轴 $(0,0)$
(2)0 大 0
(3)$<0$
(4)$=$
(5)$<$
(6)$>$
(7)$y = \frac{2}{3}x^{2}$
(1)下 $y$ 轴 $(0,0)$
(2)0 大 0
(3)$<0$
(4)$=$
(5)$<$
(6)$>$
(7)$y = \frac{2}{3}x^{2}$
2. 在抛物线①$y= 3x^{2}$,②$y= \frac {3}{2}x^{2}$,③$y= -2x^{2}$中,开口大小的顺序是()
A. ①>②>③
B. ①>③>②
C. ③>②>①
D. ②>③>①
A. ①>②>③
B. ①>③>②
C. ③>②>①
D. ②>③>①
答案:
D
3. 已知抛物线$y= ax^{2}经过点A(2,-1)$。
(1)求此抛物线的函数解析式;
(2)判断点$B(-1,2)$是否在此抛物线上。
(1)求此抛物线的函数解析式;
(2)判断点$B(-1,2)$是否在此抛物线上。
答案:
(1)$y = -\frac{1}{4}x^{2}$
(2)不在
(1)$y = -\frac{1}{4}x^{2}$
(2)不在
查看更多完整答案,请扫码查看


