《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

阅读教材 $ P_{113} \sim P_{114} $ 内容,归纳结论：
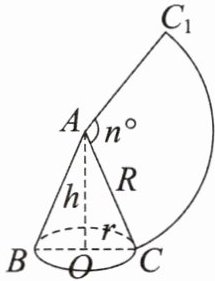
如图,沿着圆锥的一条母线,把一个圆锥的侧面展开得到一个扇形,若圆锥的底面圆的半径为 $ r $,母线长为 $ R $,扇形圆心角为 $ n^{\circ} $,则扇形的弧长为 $ $ $ = $ $ $；圆锥的侧面积为 $ $ $ = $ $ $；圆锥的全面积为 $ $；圆锥的高 $ h = $ $ $；圆心角 $ n^{\circ} = $ $ $。

答案： $\frac { n π R } { 180 } 、$2 π r 、$\frac { n π R ^ { 2 } } { 360 } 、$π R r 、π r ( r + R ) 、$\sqrt { R ^ { 2 } - r ^ { 2 } } 、$$\frac { 360 r } { R }$

1. 已知圆锥的底面半径为 3,母线长为 5,则圆锥的侧面积为()
A. 15
B. 8
C. $ 15\pi $
D. $ 8\pi $

答案： C

2. 已知圆锥的侧面积为 $ 15\pi \mathrm{cm}^{2} $,底面半径为 $ 3 \mathrm{cm} $,则圆锥的高是()
A. $ 3 \mathrm{cm} $
B. $ 4 \mathrm{cm} $
C. $ 5 \mathrm{cm} $
D. $ 8 \mathrm{cm} $

答案： B

3. 如图,已知扇形 $ AOB $ 的半径为 $ 6 \mathrm{cm} $,圆心角的度数为 $ 120^{\circ} $,若将此扇形围成一个圆锥的侧面,则围成的圆锥底面圆的半径为()

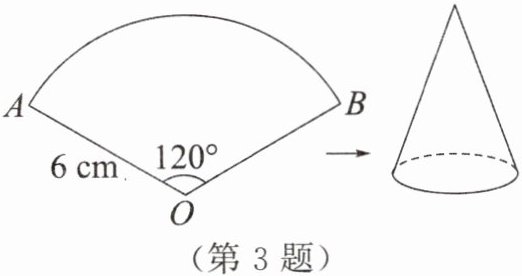
A. $ 1 \mathrm{cm} $
B. $ 2 \mathrm{cm} $
C. $ 3 \mathrm{cm} $
D. $ 4 \mathrm{cm} $

答案： B

4. (教材 $ P_{114} $ 练习 $ T_{1} $) 圆锥的底面直径是 $ 80 \mathrm{cm} $,母线长 $ 90 \mathrm{cm} $。求它的侧面展开图的圆心角和圆锥的全面积。

答案： 侧面展开图的圆心角为 160°，圆锥的全面积为 5 200 π cm²

5. (教材 $ P_{114} $ 练习 $ T_{2} $) 如图,圆锥形的烟囱帽的底面圆的直径是 $ 80 \mathrm{cm} $,母线长是 $ 50 \mathrm{cm} $,制作 100 个这样的烟囱帽至少需要多少平方米的铁皮？

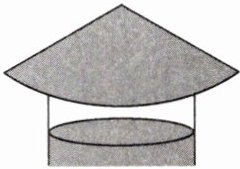
答案： 20 π m²