《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

阅读教材$P_{111}\sim P_{113}$内容,归纳结论：
1. 在半径为$R$的圆中,$n^{\circ}$的圆心角所对的弧长公式为____。
2. 在半径为$R$的圆中,圆心角为$n^{\circ}$的扇形面积公式为____；已知扇形的弧长$l和半径R$,扇形的面积公式为____。

答案： 1. $ l = \frac { n \pi R } { 180 } $ 2. $ S _ { \text { 扇形 } } = \frac { n \pi R ^ { 2 } } { 360 } $ $ S _ { \text { 扇形 } } = \frac { 1 } { 2 } l R $

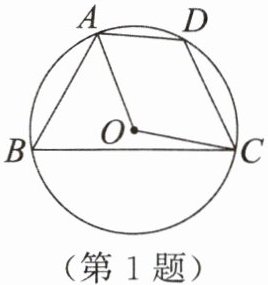
1. 如图,四边形$ABCD内接于\odot O$,若$\odot O的半径为4$,$\angle D = 120^{\circ}$,则$\overset{\frown}{AC}$的长是()

A. $\pi$
B. $\frac{4}{3}\pi$
C. $\frac{8}{3}\pi$
D. $4\pi$

答案： C

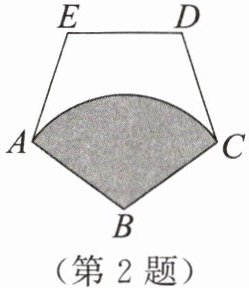
2. 如图,正五边形$ABCDE的边长为2$,若以$B$为圆心,以$BA为半径作\overset{\frown}{AC}$,则阴影部分的面积为()

A. $\frac{5\pi}{6}$
B. $\frac{4\pi}{3}$
C. $\frac{7\pi}{6}$
D. $\frac{6\pi}{5}$

答案： D

3. 若一个扇形的面积是$24\pi$,弧长是$2\pi$,则这个扇形的半径为()
A. $24$
B. $22$
C. $12$
D. $6$

答案： A

4. 已知一个扇形的圆心角为$60^{\circ}$,其弧长为$\frac{\pi}{3}cm$,求该扇形的面积。

答案： $ \frac { \pi } { 6 } \mathrm { cm } ^ { 2 } $

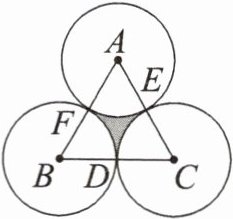
5. (教材$P_{113}练习T_{3}$改编)如图,正三角形$ABC的边长为2$,$D$,$E$,$F分别为BC$,$CA$,$AB$的中点,以$A$,$B$,$C$三点为圆心,$1$为半径作圆。求图中阴影部分的面积。

答案： $ \frac { 2 \sqrt { 3 } - \pi } { 2 } $