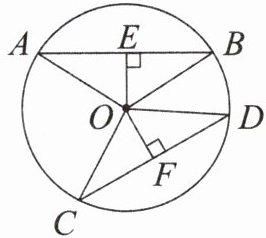
1. (教材 $ P_{85} $ 练习 $ T_1 $) 如图,$ AB $,$ CD $ 是 $ \odot O $ 的两条弦.
(1) 如果 $ AB = CD $,那么____,____.
(2) 如果 $ \overset{\frown}{AB} = \overset{\frown}{CD} $,那么____,____.
(3) 如果 $ \angle AOB = \angle COD $,那么____,____.
(4) 如果 $ AB = CD $,$ OE \perp AB $,$ OF \perp CD $,垂足分别为 $ E $,$ F $,$ OE $ 与 $ OF $ 相等吗?为什么?
(1) 如果 $ AB = CD $,那么____,____.
(2) 如果 $ \overset{\frown}{AB} = \overset{\frown}{CD} $,那么____,____.
(3) 如果 $ \angle AOB = \angle COD $,那么____,____.
(4) 如果 $ AB = CD $,$ OE \perp AB $,$ OF \perp CD $,垂足分别为 $ E $,$ F $,$ OE $ 与 $ OF $ 相等吗?为什么?

答案:
(1)$\overset{\frown}{AB}=\overset{\frown}{CD}$ $\angle AOB=\angle COD$
(2)$AB=CD$ $\angle AOB=\angle COD$
(3)$AB=CD$ $\overset{\frown}{AB}=\overset{\frown}{CD}$
(4)OE 与 OF 相等,理由略
(1)$\overset{\frown}{AB}=\overset{\frown}{CD}$ $\angle AOB=\angle COD$
(2)$AB=CD$ $\angle AOB=\angle COD$
(3)$AB=CD$ $\overset{\frown}{AB}=\overset{\frown}{CD}$
(4)OE 与 OF 相等,理由略
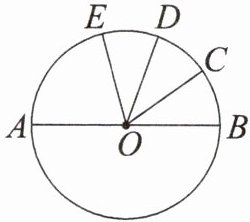
2. (教材 $ P_{85} $ 练习 $ T_2 $) 如图,$ AB $ 是 $ \odot O $ 的直径,$ \overset{\frown}{BC} = \overset{\frown}{CD} = \overset{\frown}{DE} $,$ \angle COD = 35^{\circ} $. 求 $ \angle AOE $ 的度数.

答案:
$75^{\circ}$
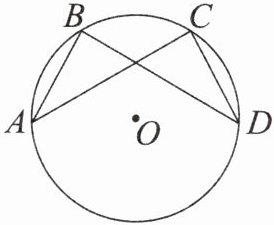
3. (教材 $ P_{89} T_4 $ 变式) 如图,$ A $,$ B $,$ C $,$ D $ 是 $ \odot O $ 上的四个点,$ AB = DC $. 求证:$ AC = BD $.

答案:
【解析】:
因为$AB = DC$,根据在同圆或等圆中,相等的弦所对的弧相等,所以$\overset{\frown}{AB}=\overset{\frown}{DC}$。
那么$\overset{\frown}{AB}+\overset{\frown}{BC}=\overset{\frown}{DC}+\overset{\frown}{BC}$(等式性质,在弧的关系中同样适用),即$\overset{\frown}{AC}=\overset{\frown}{BD}$。
再根据在同圆或等圆中,相等的弧所对的弦相等,所以$AC = BD$。
【答案】:
$\because AB = DC$,$\therefore\overset{\frown}{AB}=\overset{\frown}{DC}$,$\therefore\overset{\frown}{AB}+\overset{\frown}{BC}=\overset{\frown}{DC}+\overset{\frown}{BC}$,即$\overset{\frown}{AC}=\overset{\frown}{BD}$,$\therefore AC = BD$。
因为$AB = DC$,根据在同圆或等圆中,相等的弦所对的弧相等,所以$\overset{\frown}{AB}=\overset{\frown}{DC}$。
那么$\overset{\frown}{AB}+\overset{\frown}{BC}=\overset{\frown}{DC}+\overset{\frown}{BC}$(等式性质,在弧的关系中同样适用),即$\overset{\frown}{AC}=\overset{\frown}{BD}$。
再根据在同圆或等圆中,相等的弧所对的弦相等,所以$AC = BD$。
【答案】:
$\because AB = DC$,$\therefore\overset{\frown}{AB}=\overset{\frown}{DC}$,$\therefore\overset{\frown}{AB}+\overset{\frown}{BC}=\overset{\frown}{DC}+\overset{\frown}{BC}$,即$\overset{\frown}{AC}=\overset{\frown}{BD}$,$\therefore AC = BD$。
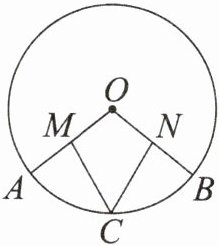
4. 能力提升 如图,已知 $ OA $,$ OB $ 是 $ \odot O $ 的半径,$ C $ 为 $ \overset{\frown}{AB} $ 的中点. $ M $,$ N $ 分别是 $ OA $,$ OB $ 的中点. 求证:$ MC = NC $.

答案:
【解析】:
连接$OC$。
因为$C$为$\overset{\frown}{AB}$的中点,根据圆心角、弧、弦的关系定理:在同圆或等圆中,等弧所对的圆心角相等,所以$\angle AOC=\angle BOC$。
又因为$OA = OB$,$M$,$N$分别是$OA$,$OB$的中点,所以$OM=\frac{1}{2}OA$,$ON=\frac{1}{2}OB$,则$OM = ON$。
在$\triangle OMC$和$\triangle ONC$中,
$\begin{cases}OM = ON\\\angle AOC=\angle BOC\\OC = OC\end{cases}$
根据全等三角形判定定理($SAS$:两边及其夹角对应相等的三角形全等),可得$\triangle OMC\cong\triangle ONC$。
根据全等三角形的性质:全等三角形的对应边相等,所以$MC = NC$。
【答案】:
连接$OC$。
$\because C$为$\overset{\frown}{AB}$的中点,$\therefore\angle AOC = \angle BOC$。
$\because OA = OB$,$M$,$N$分别是$OA$,$OB$的中点,$\therefore OM=\frac{1}{2}OA$,$ON=\frac{1}{2}OB$,$\therefore OM = ON$。
在$\triangle OMC$和$\triangle ONC$中,$\begin{cases}OM = ON\\\angle AOC=\angle BOC\\OC = OC\end{cases}$,$\therefore\triangle OMC\cong\triangle ONC(SAS)$,$\therefore MC = NC$。
连接$OC$。
因为$C$为$\overset{\frown}{AB}$的中点,根据圆心角、弧、弦的关系定理:在同圆或等圆中,等弧所对的圆心角相等,所以$\angle AOC=\angle BOC$。
又因为$OA = OB$,$M$,$N$分别是$OA$,$OB$的中点,所以$OM=\frac{1}{2}OA$,$ON=\frac{1}{2}OB$,则$OM = ON$。
在$\triangle OMC$和$\triangle ONC$中,
$\begin{cases}OM = ON\\\angle AOC=\angle BOC\\OC = OC\end{cases}$
根据全等三角形判定定理($SAS$:两边及其夹角对应相等的三角形全等),可得$\triangle OMC\cong\triangle ONC$。
根据全等三角形的性质:全等三角形的对应边相等,所以$MC = NC$。
【答案】:
连接$OC$。
$\because C$为$\overset{\frown}{AB}$的中点,$\therefore\angle AOC = \angle BOC$。
$\because OA = OB$,$M$,$N$分别是$OA$,$OB$的中点,$\therefore OM=\frac{1}{2}OA$,$ON=\frac{1}{2}OB$,$\therefore OM = ON$。
在$\triangle OMC$和$\triangle ONC$中,$\begin{cases}OM = ON\\\angle AOC=\angle BOC\\OC = OC\end{cases}$,$\therefore\triangle OMC\cong\triangle ONC(SAS)$,$\therefore MC = NC$。
查看更多完整答案,请扫码查看


