阅读教材$P_{87}\sim P_{88}$内容,归纳结论:
1. 如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做____,这个圆叫做这个多边形的____.
2. 圆内接四边形的对角____.
1. 如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做____,这个圆叫做这个多边形的____.
2. 圆内接四边形的对角____.
答案:
1. 圆内接多边形 外接圆
2. 互补
2. 互补
1. 如图,AB是$\odot O$的直径,C,D在$\odot O$上.若$∠CAB= 20^{\circ }$,则$∠ADC$等于 ()

A.$70^{\circ }$
B.$110^{\circ }$
C.$140^{\circ }$
D.$160^{\circ }$

A.$70^{\circ }$
B.$110^{\circ }$
C.$140^{\circ }$
D.$160^{\circ }$
答案:
B
2. 如图,四边形ABCD是$\odot O$的内接四边形,若$∠BOD= 80^{\circ }$,则$∠BCD$的度数是____.
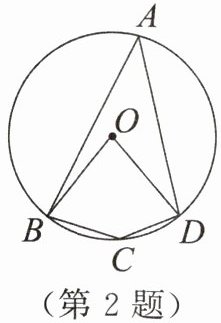

答案:
$140^{\circ}$
3. 如图,已知四边形ABCD,过点A,B,C的圆交AD于点E,连接CE,若$∠B= 70^{\circ },∠D= 80^{\circ }$,则$∠DCE$的度数为____.


答案:
$30^{\circ}$
4. 能力提升如图,$△ABC$中,$CA= CB$,以BC为直径的半圆与AB交于点D,与AC交于点E.
(1)求证:点D为AB的中点.
(2)求证:$AD= DE$.
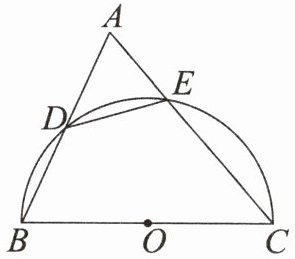
(1)求证:点D为AB的中点.
(2)求证:$AD= DE$.

答案:
【解析】:
(1) 连接$CD$,因为$BC$是半圆的直径,所以$\angle BDC = 90^{\circ}$(直径所对的圆周角是直角),即$CD\perp AB$。
又因为$CA = CB$,根据等腰三角形三线合一的性质(等腰三角形底边上的高、底边上的中线、顶角平分线互相重合),所以$AD = BD$,即点$D$为$AB$的中点。
(2) 连接$BE$、$DE$,因为$BC$是半圆的直径,所以$\angle BEC = 90^{\circ}$(直径所对的圆周角是直角),即$BE\perp AC$。
因为$CA = CB$,所以$\angle ABE=\angle CBE$(等腰三角形三线合一)。
根据同弧所对的圆周角相等,$\overset{\frown}{DE}$所对的圆周角$\angle DCE$和$\angle DBE$,$\overset{\frown}{BD}$所对的圆周角$\angle BCD$和$\angle BED$。
因为$\angle ACD=\angle BCD$(等腰三角形三线合一,$CD\perp AB$,$CA = CB$),$\angle ACD$和$\angle AED$是圆内接四边形$BCED$的一个外角和它的内对角,所以$\angle ACD=\angle AED$。
又因为$\angle DCE=\angle DBE$,$\angle BCD=\angle BED$,$\angle ACD=\angle BCD$,所以$\angle AED=\angle ADE$(等角对等边),所以$AD = DE$。
【答案】:
(1) 连接$CD$,由$BC$是直径得$\angle BDC = 90^{\circ}$,又$CA = CB$,根据等腰三角形三线合一,证得点$D$为$AB$中点。
(2) 连接$BE$、$DE$,由$BC$是直径得$\angle BEC = 90^{\circ}$,结合$CA = CB$得$\angle ABE=\angle CBE$,再利用圆周角性质及圆内接四边形外角性质,证得$\angle AED=\angle ADE$,从而$AD = DE$。
(1) 连接$CD$,因为$BC$是半圆的直径,所以$\angle BDC = 90^{\circ}$(直径所对的圆周角是直角),即$CD\perp AB$。
又因为$CA = CB$,根据等腰三角形三线合一的性质(等腰三角形底边上的高、底边上的中线、顶角平分线互相重合),所以$AD = BD$,即点$D$为$AB$的中点。
(2) 连接$BE$、$DE$,因为$BC$是半圆的直径,所以$\angle BEC = 90^{\circ}$(直径所对的圆周角是直角),即$BE\perp AC$。
因为$CA = CB$,所以$\angle ABE=\angle CBE$(等腰三角形三线合一)。
根据同弧所对的圆周角相等,$\overset{\frown}{DE}$所对的圆周角$\angle DCE$和$\angle DBE$,$\overset{\frown}{BD}$所对的圆周角$\angle BCD$和$\angle BED$。
因为$\angle ACD=\angle BCD$(等腰三角形三线合一,$CD\perp AB$,$CA = CB$),$\angle ACD$和$\angle AED$是圆内接四边形$BCED$的一个外角和它的内对角,所以$\angle ACD=\angle AED$。
又因为$\angle DCE=\angle DBE$,$\angle BCD=\angle BED$,$\angle ACD=\angle BCD$,所以$\angle AED=\angle ADE$(等角对等边),所以$AD = DE$。
【答案】:
(1) 连接$CD$,由$BC$是直径得$\angle BDC = 90^{\circ}$,又$CA = CB$,根据等腰三角形三线合一,证得点$D$为$AB$中点。
(2) 连接$BE$、$DE$,由$BC$是直径得$\angle BEC = 90^{\circ}$,结合$CA = CB$得$\angle ABE=\angle CBE$,再利用圆周角性质及圆内接四边形外角性质,证得$\angle AED=\angle ADE$,从而$AD = DE$。
查看更多完整答案,请扫码查看


