《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

阅读教材$P_{51}$内容,归纳结论:
建立适当的直角坐标系,利用二次函数解决抛物线形实际问题时,一般以该抛物线的____为原点,____为$y$轴,设抛物线的解析式为____来解决.

答案： 顶点 对称轴 $ y = ax^{2} + bx + c $

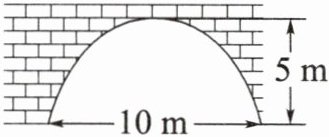
1. 一座古代拱桥的截面图如图所示,拱桥桥洞的上沿近似为抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m.
(1)以拱桥的顶点为原点,建立平面直角坐标系,求抛物线的函数解析式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.

答案：
(1)建系略；$ y = -\frac{1}{5}x^{2} $
(2)$\frac{16}{5}m$

2. 小明在一次足球训练中,从球门正前方8m的A处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.现以点O为原点,建立平面直角坐标系如图所示.

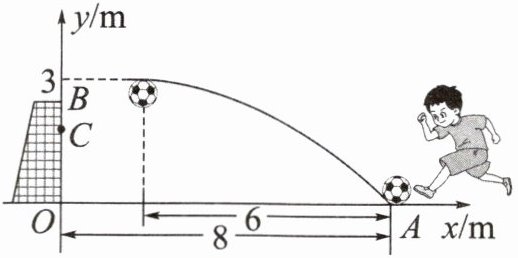
(1)求抛物线的函数解析式;
(2)已知球门OB的高度为2.44m,请通过计算判断球能否射进球门(忽略其他因素).

答案：
(1)$ y = -\frac{1}{12}(x - 2)^{2} + 3 $
(2)不能，计算略