阅读教材$P_{35}\sim P_{37}$内容,归纳结论:
二次函数$y = a(x - h)^2 + k$的开口方向由____决定,对称轴是____,顶点坐标是____。
二次函数$y = a(x - h)^2 + k$的开口方向由____决定,对称轴是____,顶点坐标是____。
答案:
$a$ $x = h$ $(h, k)$
1. 由二次函数$y = 3(x - 4)^2 - 2$可知 ()
A. 其图象的开口向下
B. 当$x > 4$时,$y随x$的增大而减小
C. 其最小值为2
D. 其图象的对称轴为直线$x = 4$
A. 其图象的开口向下
B. 当$x > 4$时,$y随x$的增大而减小
C. 其最小值为2
D. 其图象的对称轴为直线$x = 4$
答案:
D
2. 已知点$A(-2,y_1)$,$B(1,y_2)$,$C(6,y_3)都在二次函数y = -4(x - 3)^2 + 1$的图象上,则$y_1$,$y_2$,$y_3$的大小关系为 ()
A. $y_1 > y_2 > y_3$
B. $y_2 > y_1 > y_3$
C. $y_2 > y_3 > y_1$
D. $y_3 > y_2 > y_1$
A. $y_1 > y_2 > y_3$
B. $y_2 > y_1 > y_3$
C. $y_2 > y_3 > y_1$
D. $y_3 > y_2 > y_1$
答案:
C
3. 按要求画图,并回答问题。
(1)如图,在平面直角坐标系中,画出二次函数$y = -\frac{1}{2}x^2与y = -\frac{1}{2}(x + 2)^2 - 4$的图象。
列表:
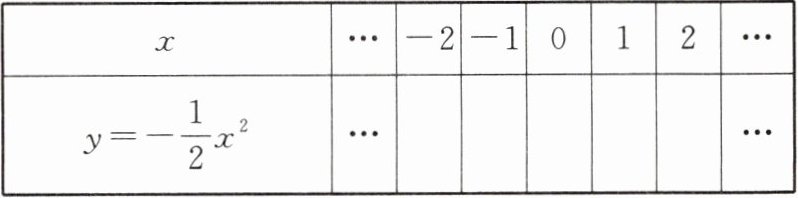
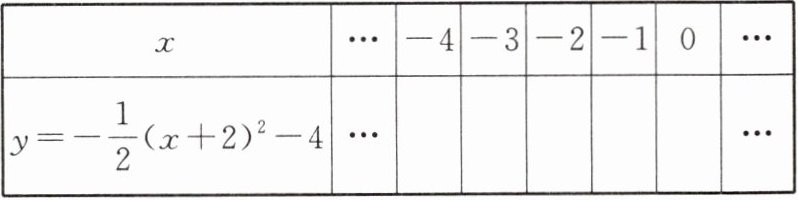
描点并连线:
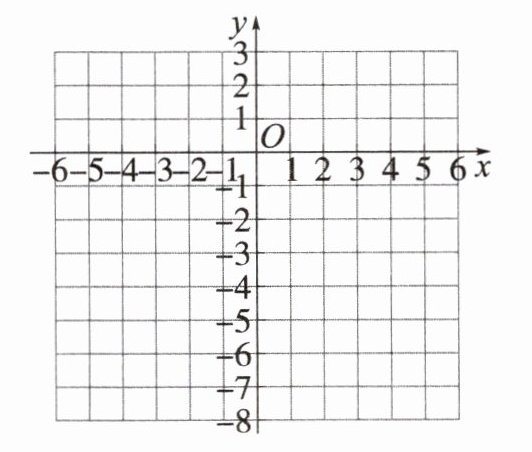
(2)函数$y = -\frac{1}{2}(x + 2)^2 - 4$的图象开口____,对称轴是____,顶点坐标是____;当$x$____时,$y随x$的增大而减小。
(3)观察(1)中的两条抛物线,将抛物线$y = -\frac{1}{2}x^2怎样移动可以得到抛物线y = -\frac{1}{2}(x + 2)^2 - 4$?
(1)如图,在平面直角坐标系中,画出二次函数$y = -\frac{1}{2}x^2与y = -\frac{1}{2}(x + 2)^2 - 4$的图象。
列表:


描点并连线:

(2)函数$y = -\frac{1}{2}(x + 2)^2 - 4$的图象开口____,对称轴是____,顶点坐标是____;当$x$____时,$y随x$的增大而减小。
(3)观察(1)中的两条抛物线,将抛物线$y = -\frac{1}{2}x^2怎样移动可以得到抛物线y = -\frac{1}{2}(x + 2)^2 - 4$?
答案:
(1)略
(2)向下 $x = -2$ $(-2, -4)$ $> -2$
(3)略
(1)略
(2)向下 $x = -2$ $(-2, -4)$ $> -2$
(3)略
4. 能力提升已知二次函数的图象经过点$(-1,6)$,且顶点坐标是$(3,2)$。
(1)求此二次函数的解析式;
(2)当$-2\leqslant x\leqslant 1$时,求函数的最小值。
(1)求此二次函数的解析式;
(2)当$-2\leqslant x\leqslant 1$时,求函数的最小值。
答案:
(1)$y = \frac{1}{4}(x - 3)^2 + 2$
(2)3
(1)$y = \frac{1}{4}(x - 3)^2 + 2$
(2)3
查看更多完整答案,请扫码查看


