阅读教材 $P_{105}\sim P_{108}$ 内容,归纳结论:
1. 如图,一个正多边形的外接圆的圆心叫做这个正多边形的______,外接圆的半径叫做正多边形的______,正多边形每一边所对的圆心角叫做正多边形的______,中心到正多边形的一边的距离叫做正多边形的______。
2. 所有的正多边形都是轴对称图形,一个 $n$ 边形,共有______条对称轴;一个正 $n$ 边形,若 $n$ 为偶数,则该多边形______中心对称图形;若 $n$ 为奇数,则该多边形______中心对称图形。
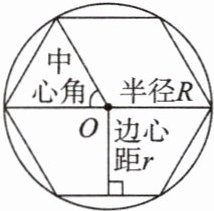
1. 如图,一个正多边形的外接圆的圆心叫做这个正多边形的______,外接圆的半径叫做正多边形的______,正多边形每一边所对的圆心角叫做正多边形的______,中心到正多边形的一边的距离叫做正多边形的______。
2. 所有的正多边形都是轴对称图形,一个 $n$ 边形,共有______条对称轴;一个正 $n$ 边形,若 $n$ 为偶数,则该多边形______中心对称图形;若 $n$ 为奇数,则该多边形______中心对称图形。

答案:
1. 中心 半径 中心角 边心距
2. $ n $ 是 不是
2. $ n $ 是 不是
1. 如图,正五边形 $ABCDE$ 内接于 $\odot O$,点 $F$ 是 $\overset{\frown}{DE}$ 上的动点,则 $\angle AFC$ 的度数为()

A. $60^{\circ}$
B. $72^{\circ}$
C. $144^{\circ}$
D. 随着点 $F$ 的变化而变化

A. $60^{\circ}$
B. $72^{\circ}$
C. $144^{\circ}$
D. 随着点 $F$ 的变化而变化
答案:
B
2. 如图,$A$,$B$,$C$,$D$ 为一个正多边形的顶点,$O$ 为正多边形的中心. 若 $\angle ADB = 18^{\circ}$,则这个正多边形的边数为()
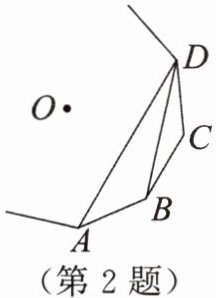
A. $7$
B. $8$
C. $9$
D. $10$

A. $7$
B. $8$
C. $9$
D. $10$
答案:
D
3. (教材 $P_{108}$ 习题 $T_{1}$ 改编)完成下表中有关正多边形的计算:



答案:
【解析】:
- 对于正三角形:
中心角:$360^{\circ}\div3 = 120^{\circ}$。
设半径为$R$,边心距为$r$,边长为$a$。由$\frac{a}{2}=R\sin60^{\circ}$,已知$a = 2\sqrt{3}$,则$\frac{2\sqrt{3}}{2}=R\times\frac{\sqrt{3}}{2}$,解得$R = 2$;$r=R\cos60^{\circ}=2\times\frac{1}{2}=1$;周长$C = 3a=3\times2\sqrt{3}=6\sqrt{3}$;面积$S=\frac{1}{2}Cr=\frac{1}{2}\times6\sqrt{3}\times1 = 3\sqrt{3}$。
对于正方形:
内角:$\frac{(4 - 2)\times180^{\circ}}{4}=90^{\circ}$;中心角:$360^{\circ}\div4 = 90^{\circ}$。
已知边心距$r = 1$,因为正方形中$R=\sqrt{2}r$,所以$R=\sqrt{2}$;边长$a = 2r=2$;周长$C = 4a=8$;面积$S=\frac{1}{2}Cr=\frac{1}{2}\times8\times1 = 4$。
对于正六边形:
内角:$\frac{(6 - 2)\times180^{\circ}}{6}=120^{\circ}$;中心角:$360^{\circ}\div6 = 60^{\circ}$。
已知边心距$r=\sqrt{3}$,因为正六边形中$R = 2$($r = R\cos30^{\circ}$,$\sqrt{3}=R\times\frac{\sqrt{3}}{2}$);边长$a = R = 2$;周长$C = 6a=12$;面积$S=\frac{1}{2}Cr=\frac{1}{2}\times12\times\sqrt{3}=6\sqrt{3}$。
【答案】:
|正多边形边数|内角|中心角|半径|边长|边心距|周长|面积|
|----|----|----|----|----|----|----|----|
| $3$ | $60^{\circ}$ | $120^{\circ}$ | $2$ | $2\sqrt{3}$ | $1$ | $6\sqrt{3}$ | $3\sqrt{3}$ |
| $4$ | $90^{\circ}$ | $90^{\circ}$ | $\sqrt{2}$ | $2$ | $1$ | $8$ | $4$ |
| $6$ | $120^{\circ}$ | $60^{\circ}$ | $2$ | $2$ | $\sqrt{3}$ | $12$ | $6\sqrt{3}$ |
- 对于正三角形:
中心角:$360^{\circ}\div3 = 120^{\circ}$。
设半径为$R$,边心距为$r$,边长为$a$。由$\frac{a}{2}=R\sin60^{\circ}$,已知$a = 2\sqrt{3}$,则$\frac{2\sqrt{3}}{2}=R\times\frac{\sqrt{3}}{2}$,解得$R = 2$;$r=R\cos60^{\circ}=2\times\frac{1}{2}=1$;周长$C = 3a=3\times2\sqrt{3}=6\sqrt{3}$;面积$S=\frac{1}{2}Cr=\frac{1}{2}\times6\sqrt{3}\times1 = 3\sqrt{3}$。
对于正方形:
内角:$\frac{(4 - 2)\times180^{\circ}}{4}=90^{\circ}$;中心角:$360^{\circ}\div4 = 90^{\circ}$。
已知边心距$r = 1$,因为正方形中$R=\sqrt{2}r$,所以$R=\sqrt{2}$;边长$a = 2r=2$;周长$C = 4a=8$;面积$S=\frac{1}{2}Cr=\frac{1}{2}\times8\times1 = 4$。
对于正六边形:
内角:$\frac{(6 - 2)\times180^{\circ}}{6}=120^{\circ}$;中心角:$360^{\circ}\div6 = 60^{\circ}$。
已知边心距$r=\sqrt{3}$,因为正六边形中$R = 2$($r = R\cos30^{\circ}$,$\sqrt{3}=R\times\frac{\sqrt{3}}{2}$);边长$a = R = 2$;周长$C = 6a=12$;面积$S=\frac{1}{2}Cr=\frac{1}{2}\times12\times\sqrt{3}=6\sqrt{3}$。
【答案】:
|正多边形边数|内角|中心角|半径|边长|边心距|周长|面积|
|----|----|----|----|----|----|----|----|
| $3$ | $60^{\circ}$ | $120^{\circ}$ | $2$ | $2\sqrt{3}$ | $1$ | $6\sqrt{3}$ | $3\sqrt{3}$ |
| $4$ | $90^{\circ}$ | $90^{\circ}$ | $\sqrt{2}$ | $2$ | $1$ | $8$ | $4$ |
| $6$ | $120^{\circ}$ | $60^{\circ}$ | $2$ | $2$ | $\sqrt{3}$ | $12$ | $6\sqrt{3}$ |
4. 请用圆规和直尺作图,不写作法,但要保留作图痕迹.
已知:如图,点 $A$ 在 $\odot O$ 上.
求作:以 $A$ 为一顶点,作圆内接正方形 $ABCD$.
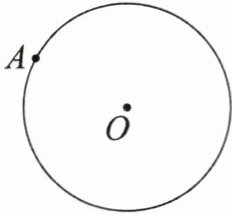
已知:如图,点 $A$ 在 $\odot O$ 上.
求作:以 $A$ 为一顶点,作圆内接正方形 $ABCD$.

答案:
【解析】:
1. 连接 $OA$,并延长 $AO$ 交 $\odot O$ 于点 $C$。
理由:圆的直径是通过圆心的弦,这样就得到了圆的一条直径 $AC$。
2. 作 $AC$ 的垂直平分线,分别交 $\odot O$ 于点 $B$、$D$。
理由:垂直平分直径的弦与该直径互相垂直且相等(在圆中,直径所对圆周角是直角,利用垂直平分线性质可得到正方形的边)。
3. 连接 $AB$、$BC$、$CD$、$DA$,则四边形 $ABCD$ 就是所求作的圆内接正方形。
理由:根据圆内接正方形的性质,对角线互相垂直且相等的四边形是正方形,这里 $AC$、$BD$ 是圆的直径且互相垂直,$AB = BC = CD = DA$(同圆中,等弧所对弦相等)。
【答案】:按上述步骤作图,保留作图痕迹,作出圆内接正方形 $ABCD$。
1. 连接 $OA$,并延长 $AO$ 交 $\odot O$ 于点 $C$。
理由:圆的直径是通过圆心的弦,这样就得到了圆的一条直径 $AC$。
2. 作 $AC$ 的垂直平分线,分别交 $\odot O$ 于点 $B$、$D$。
理由:垂直平分直径的弦与该直径互相垂直且相等(在圆中,直径所对圆周角是直角,利用垂直平分线性质可得到正方形的边)。
3. 连接 $AB$、$BC$、$CD$、$DA$,则四边形 $ABCD$ 就是所求作的圆内接正方形。
理由:根据圆内接正方形的性质,对角线互相垂直且相等的四边形是正方形,这里 $AC$、$BD$ 是圆的直径且互相垂直,$AB = BC = CD = DA$(同圆中,等弧所对弦相等)。
【答案】:按上述步骤作图,保留作图痕迹,作出圆内接正方形 $ABCD$。
查看更多完整答案,请扫码查看


