《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

阅读教材$P_{43}\sim P_{45}$内容,归纳结论:
1. 若一元二次方程$ax^{2}+bx+c= 0的两根为x_{1},x_{2}$,则抛物线$y= ax^{2}+bx+c$与x轴的两个交点坐标分别是______.
2. 抛物线$y= ax^{2}+bx+c$与x轴的交点个数由______的符号决定.
3. 抛物线$y= ax^{2}+bx+c$与y轴的交点坐标为______.

答案： 1. $(x_{1},0),(x_{2},0)$
2. $b^{2}-4ac$
3. $(0,c)$

1. 已知二次函数$y= ax^{2}+bx+c$的部分图象如图所示,则关于x的一元二次方程$ax^{2}+bx+c= 0$的根为 ()

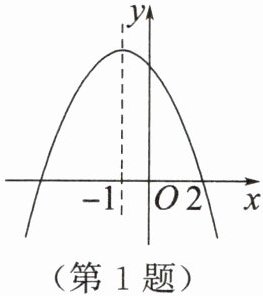
A. $x_{1}= -4,x_{2}= 2$
B. $x_{1}= -3,x_{2}= -1$
C. $x_{1}= -4,x_{2}= -2$
D. $x_{1}= -2,x_{2}= 2$

答案： A

2. 已知二次函数$y= x^{2}+bx+c$的部分对应值如下表:

根据表中数据,关于x的一元二次方程$x^{2}+bx+c= 0$的解为 ()
A. $x_{1}= -1,x_{2}= -3$
B. $x_{1}= -1,x_{2}= 1$
C. $x_{1}= -1,x_{2}= 3$
D. $x_{1}= -1,x_{2}= 5$

答案： C

3. (教材$P_{47}T_{3}$改编)一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是$y= -\frac {1}{12}x^{2}+\frac {2}{3}x+\frac {5}{3}$,则铅球推出的距离为______m.

答案： 10

4. 已知二次函数$y= x^{2}-6x+m$的图象与x轴只有一个公共点,求m的值,并求出这个公共点的坐标.

答案： $m=9$；公共点的坐标为$(3,0)$

5. 能力提升已知二次函数$y= -x^{2}-(m-1)x+m+1$.
(1) 求证:不论m取何值,该函数图象与x轴总有两个交点;
(2) 若该函数图象的对称轴是直线$x= 2$,求该函数的图象与y轴的交点坐标.

答案：
(1)略
(2)$(0,-2)$