《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

1. (教材$P_{42}T_{2}$)根据下列条件,判断$△ABC与△A'B'C'$是否相似,并说明理由:
(1)$AB= 10cm,BC= 12cm,AC= 15cm,A'B'= 150cm,B'C'= 180cm,A'C'= 225cm;$
(2)$∠A= 70^{\circ },∠B= 48^{\circ },∠A'= 70^{\circ },∠C'= 62^{\circ }.$

答案：
(1)$\triangle ABC\backsim \triangle A'B'C'$，理由略
(2)$\triangle ABC\backsim \triangle A'B'C'$，理由略

2. (教材$P_{57}T_{3}$)根据下列图中所注的条件,判断图中两个三角形是否相似,并求出x和y的值.

答案：
(1)$\triangle FGH\backsim \triangle JIH$，$x=4$，$y=10$
(2)$\triangle FGH\backsim \triangle JKH$，$x=124$，$y=33$![img alt=3]

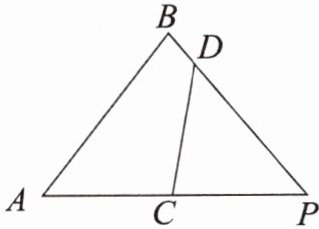
3. 能力提升如图,在$△ABP$中,C,D分别是AP,BP上的点.已知$CD= CP= 4,DP= 5,AC= 3.5,BD= 1.$
(1)求证:$△ABP\backsim △DCP;$
(2)求AB的长.

答案：
(1)略
(2)6