阅读教材$P_{46}$内容,归纳结论:
1. 二次函数与一元二次方程有着密切的关系,我们可以根据二次函数的图象近似地求一元二次方程的____,也可以通过一元二次方程求二次函数的图象与$x$轴公共点的____坐标.
2. 二次函数的图象位于$x$轴下方,表示$y$____$0$;二次函数的图象位于$x$轴上方,表示$y$____$0$.
1. 二次函数与一元二次方程有着密切的关系,我们可以根据二次函数的图象近似地求一元二次方程的____,也可以通过一元二次方程求二次函数的图象与$x$轴公共点的____坐标.
2. 二次函数的图象位于$x$轴下方,表示$y$____$0$;二次函数的图象位于$x$轴上方,表示$y$____$0$.
答案:
1. 根 横
2. < >
2. < >
1. 如图,二次函数$y = ax^{2}+bx + c的部分图象与y轴的交点为(0,3)$,若它的对称轴为直线$x = 1$,则方程$ax^{2}+bx + c = 0$的其中一个根在()
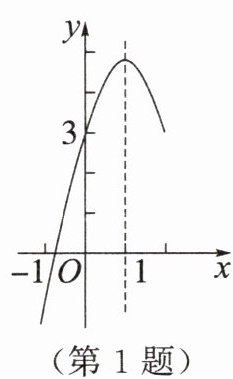
A. 1和2之间
B. 2和3之间
C. 3和4之间
D. 4和5之间

A. 1和2之间
B. 2和3之间
C. 3和4之间
D. 4和5之间
答案:
B
2. 二次函数$y = ax^{2}+bx + c$图象的一部分如图所示,其对称轴为$x = 1$,若其与$x轴的交点为A(3,0)$,则由图象可知,不等式$ax^{2}+bx + c\geqslant0$的解集是____.
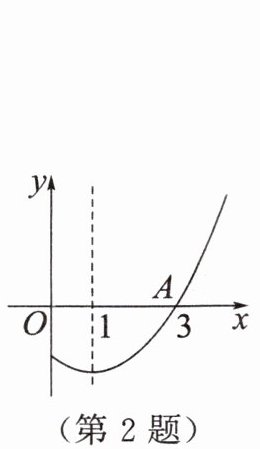

答案:
$ x \leq -1 $ 或 $ x \geq 3 $
3. (教材$P_{47}T_{5}$改编)如图,在平面直角坐标系中,画出函数$y = x^{2}-2x - 3$的图象,利用图象回答:
(1)方程$x^{2}-2x - 3 = 0$的解是____;
(2)当$y>0$时,自变量$x$的取值范围是____;
(3)当$y<0$时,自变量$x$的取值范围是____.
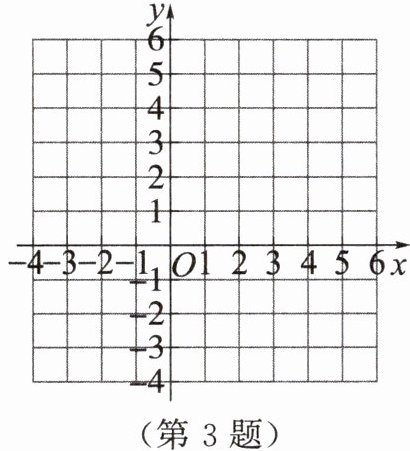
(1)方程$x^{2}-2x - 3 = 0$的解是____;
(2)当$y>0$时,自变量$x$的取值范围是____;
(3)当$y<0$时,自变量$x$的取值范围是____.

答案:
图略
(1) $ x_1 = -1 $,$ x_2 = 3 $
(2) $ x < -1 $ 或 $ x > 3 $
(3) $ -1 < x < 3 $
(1) $ x_1 = -1 $,$ x_2 = 3 $
(2) $ x < -1 $ 或 $ x > 3 $
(3) $ -1 < x < 3 $
4. 已知二次函数$y = ax^{2}+bx + c$的部分图象如图所示.
(1)求该函数图象与$x$轴的另一个交点坐标;
(2)求这个二次函数的解析式;
(3)直接写出满足$y<0时x$的取值范围;
(4)能力提升求不等式$ax^{2}+bx + c\leqslant12$的解集.
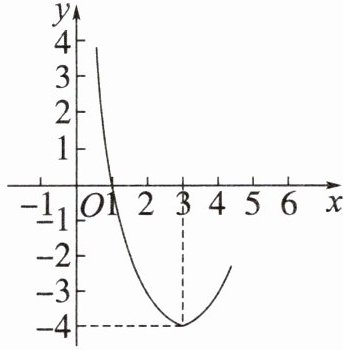
(1)求该函数图象与$x$轴的另一个交点坐标;
(2)求这个二次函数的解析式;
(3)直接写出满足$y<0时x$的取值范围;
(4)能力提升求不等式$ax^{2}+bx + c\leqslant12$的解集.

答案:
(1) $ (5, 0) $
(2) $ y = (x - 3)^2 - 4 $
(3) $ 1 < x < 5 $
(4) $ -1 \leq x \leq 7 $
(1) $ (5, 0) $
(2) $ y = (x - 3)^2 - 4 $
(3) $ 1 < x < 5 $
(4) $ -1 \leq x \leq 7 $
查看更多完整答案,请扫码查看


