《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

阅读教材$P_{64}\sim P_{66}$内容,归纳结论：
1. 把一个图形绕着某一点旋转$180^{\circ }$,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或______,这个点叫做______。
2. 中心对称的性质：
中心对称的两个图形,对称点所连线段都经过______,而且被______所平分；中心对称的两个图形是______图形。

答案： 知识梳理
1. 中心对称 对称中心
2. 对称中心 对称中心 全等

1. 如图,$\triangle ABC与\triangle A'B'C'关于点O$中心对称,下列结论不成立的是()

A. $OB= OB'$
B. $BC// B'C'$
C. 点$A的对称点是点A'$
D. $∠ACB= ∠A'B'C'$

答案： 随堂检测
1. D

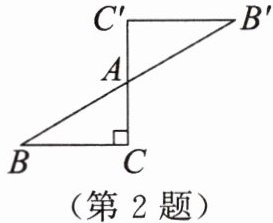
2. 如图,$Rt\triangle ABC与Rt\triangle AB'C'关于点A$中心对称。若$∠C= 90^{\circ },∠B= 30^{\circ },AC= \sqrt {3}$,则$BB'$的长为______。

答案： 随堂检测
2. $4\sqrt{3}$

3. 分别画出下列图形关于点$O$对称的图形(尺规作图,不写作法,保留作图痕迹)。

答案： 随堂检测
3. 略

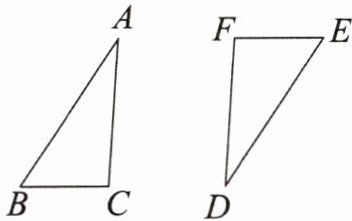
4. 如图,$\triangle ABC和\triangle DEF关于点O$中心对称。
(1)画出它们的对称中心点$O$；
(2)若$AB= 6,AC= 5,BC= 3$,求$\triangle DEF$的周长；
(3)连接$AF$,$CD$,判断四边形$ACDF$的形状,并说明理由。

答案： 随堂检测
4.
(1)略
(2)14
(3)四边形 $ACDF$ 为平行四边形，理由略