《2025年海淀单元测试AB卷七年级数学下册沪科版》

五、（本题满分12分）
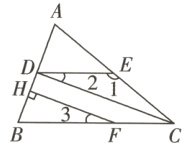
19. 新教材 变式题（马鞍山期末）如图，已知∠1=142°，∠ACB=38°，CD平分∠ACB，∠2=∠3，FH⊥AB于点H.
（1）AB与CD是否垂直？请说明理由.
（2）求∠ADE的度数.

答案： 解：
(1)AB与CD垂直.理由如下：
∵∠1=142°，∠ACB=38°，
∴∠1 + ∠ACB=180°，
∴DE//BC，
∴∠2=∠DCB.又
∵∠2=∠3，
∴∠3=∠DCB，
∴HF//CD，
∴∠BHF=∠BDC.又
∵FH⊥AB，
∴∠BDC=∠BHF=90°，
∴CD⊥AB.
(2)
∵CD平分∠ACB，∠ACB=38°，
∴∠DCB=19°.
∵∠BDC=90°，
∴∠B=180° - 90° - 19°=71°.
∵DE//BC，
∴∠ADE=∠B=71°.

六、（本题满分12分）
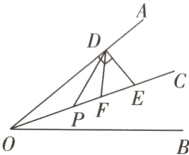
20. （合肥期中）如图，∠AOB=40°，OC平分∠AOB，点E在射线OC上，ED⊥OA，垂足为点D，DF平分∠ODE，交射线OC于点F，动点P从点O出发沿射线OC运动，连接DP.
（1）当DP平分∠ODF时，∠PDE=________°.
（2）当DP//OB时，求∠PDE的度数.
（3）当DP⊥FD时，求∠ADP的度数.

答案：
解：
(1)
∵ED⊥OA，
∴∠ODE=90°.
∵DF平分∠ODE，
∴∠ODF=∠EDF=$\frac{1}{2}$∠ODE=45°.
∵PD平分∠ODF，
∴∠PDF=$\frac{1}{2}$∠ODF=22.5°，
∴∠PDE=∠PDF + ∠EDF=67.5°.故答案为67.5.
(2)如图，DP//OB.
∵DP//OB，
∴∠AOB + ∠ODP=180°.
∵∠AOB=40°，
∴∠ODP=140°，
∴∠PDE=∠ODP - ∠ODE=140° - 90°=50°.
(3)如图，DP⊥FD.
∵DP⊥FD，
∴∠PDF=90°，
∴∠ADP=180° - ∠ODF - ∠PDF=180° - 45° - 90°=45°.

七、（本题满分12分）
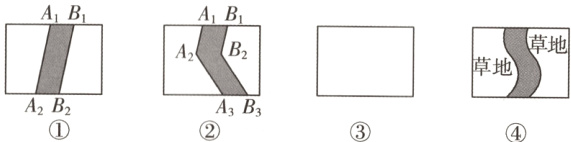
21. 新动向 探究题 如图，图形的操作过程（四个长方形的水平方向的长均为a，竖直方向的宽均为b）：将线段A₁A₂向右平移1个单位长度到B₁B₂，得到封闭图形A₁A₂B₂B₁（即图①中的阴影部分）；将折线A₁A₂A₃向右平移1个单位长度到B₁B₂B₃，得到封闭图形A₁A₂A₃B₃B₂B₁（即图②中的阴影部分）.
（1）在图③中，请你类似地画出一条有两个折点的折线，同样向右平移1个单位长度，从而得到一个封闭图形，并画出阴影部分.
（2）请你分别写出上述三个图形除阴影部分外剩余部分的面积S₁=________，S₂=________，S₃=________.
（3）联想与探究：如图④，在一长方形草地上，有一条弯曲的柏油小路（小路任何地方的水平宽度都是1个单位长度），请你猜想空白部分草地的面积是多少，并说明你猜想的理由.

答案：
解：
(1)如图所示.(答案不唯一)

(2)ab - b ab - b ab - b
(3)草地的面积为ab - b.理由：将左边草地向右平移1个单位长度就可得到一个水平方向长为a - 1、竖直方向宽为b的长方形草地.草地面积为(a - 1)b=ab - b.