《2025年海淀单元测试AB卷七年级数学下册沪科版》

9.(绵阳中考变式)正整数a，b分别满足$\sqrt[3]{53}＜a＜\sqrt[3]{98}$，$\sqrt{2}＜b＜\sqrt{7}$，则ab的立方根是( )
A. 2
B. 4
C. 8
D. 16

答案： A [解析]
∵$\sqrt[3]{53}＜\sqrt[3]{64}＜\sqrt[3]{98}$,$\sqrt{2}＜\sqrt{4}＜\sqrt{7}$,
∴a = 4,b = 2,
∴ab = 4×2 = 8,
∵$\sqrt[3]{8}=2$,
∴ab的立方根是2.故选A.

10. 新考向 规律探究 将一组数$\sqrt{3}$，$\sqrt{6}$，3，$\sqrt{12}$，$\sqrt{15}$，…，$\sqrt{228}$按下面的方法进行排列：
$\sqrt{3}$，$\sqrt{6}$，3，$\sqrt{12}$，$\sqrt{15}$，
$\sqrt{18}$，$\sqrt{21}$，$\sqrt{24}$，$\sqrt{27}$，$\sqrt{30}$，
…
若$\sqrt{12}$的位置记为(1，4)，$\sqrt{24}$的位置记为(2，3)，则这组数中最大的有理数的位置记为( )
A.(14，4)
B.(14，5)
C.(15，5)
D.(16，1)

答案： C [解析]这组数可写为$\sqrt{3×1}$,$\sqrt{3×2}$,$\sqrt{3×3}$,$\sqrt{3×4}$,$\sqrt{3×5}$,… ,$\sqrt{3×76}$.又
∵$\sqrt{225}=15$是有理数,$\sqrt{225}=\sqrt{3×75}$,75÷5 = 15,且由题意可得，每五个数为一行，
∴$\sqrt{225}$为第15行，从左数第5个数,即这组数中最大的有理数$\sqrt{225}$的位置记为(15,5).故选C;

11. 辨思维 平方法(安徽中考)我国古代数学家张衡将圆周率取值为$\sqrt{10}$，祖冲之给出圆周率的一种分数形式的近似值为$\frac{22}{7}$.比较大小：$\sqrt{10}$______$\frac{22}{7}$.(填“＞”或“＜”)

答案： ＞ [解析]($\sqrt{10}$)² = 10,($\frac{22}{7}$)² = $\frac{484}{49}$.
∵10＞$\frac{484}{49}$,
∴$\sqrt{10}$＞$\frac{22}{7}$.

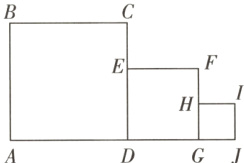
12. 新考向 开放题(深圳中考)如图所示，四边形ABCD，DEFG，GHIJ均为正方形，且$S_{正方形ABCD}=10$，$S_{正方形GHIJ}=1$，则正方形DEFG的边长可以是______.(写出一个答案即可)

答案： 2(答案不唯一) [解析]
∵S正方形ABCD = 10,S正方形GHIJ = 1,
∴AD = $\sqrt{10}$,GJ = 1,
∴1＜DG＜$\sqrt{10}$,
∴正方形DEFG的边长可以是2.

13. 新教材 变式题(合肥期中)把两个半径分别为1 cm和$\sqrt[3]{7}$cm的铅球熔化后做成一个更大的铅球，则这个大铅球的半径是______ cm.(球的体积公式$V=\frac{4}{3}\pi r^3$，其中r是球的半径)

答案：
2 [解析]$\frac{4}{3}$π×1³ + $\frac{4}{3}$π×(3π)² = $\frac{32}{3}$π(cm²),大铅球的半径为$\frac{32}{3}$π = 2(cm).故答案为2.

14. 新课标 运算能力 任何实数a，可用$[a]$表示不超过a的最大整数.如$[4]=4$，$[\sqrt{3}]=1$.现对72进行如下操作：$72\xrightarrow{第1次}[\sqrt{72}]=8\xrightarrow{第2次}[\sqrt{8}]=2\xrightarrow{第3次}[\sqrt{2}]=1$，这样对72只需进行3次操作后变为1.类似地：
(1)对81只需进行______次操作后变为1.
(2)只需进行3次操作后变为1的所有正整数中，最大的是______.

答案：
(1)3
(2)255 [解析]
(1)
∵[$\sqrt{81}$] = 9,[$\sqrt{9}$] = 3,[$\sqrt{3}$] = 1,
∴对$\sqrt{81}$只需进行3次操作后变为1；
(2)[$\sqrt{255}$] = 15,第1次[$\sqrt{15}$] = 3,第2次[$\sqrt{3}$] = 1；[$\sqrt{256}$] = 16,第1次[$\sqrt{16}$] = 4,第2次[$\sqrt{4}$] = 2,第3次[$\sqrt{2}$] = 1,
∴答案为255.