《2025年海淀单元测试AB卷七年级数学下册沪科版》

8. 辨思维 类比思想 (荆门中考)对于任意实数a, b, a³ + b³ = (a + b)(a² - ab + b²)恒成立,则下列关系式正确的是( )
A. a³ - b³ = (a - b)(a² + ab + b²)
B. a³ - b³ = (a + b)(a² + ab + b²)
C. a³ - b³ = (a - b)(a² - ab + b²)
D. a³ - b³ = (a + b)(a² + ab - b²)

答案： A [解析]
∵a³ + b³ = (a + b)(a² - ab + b²)，
∴a³ - b³ = a³ + (-b)³ = [a + (-b)][a² - a·(-b) + (-b)²] = (a - b)(a² + ab + b²)。故选A。

9. 新教材 变式题 如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的长方形.根据图形的变化过程写出的一个正确的等式是( )

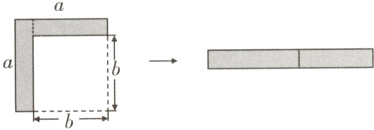
A. (a - b)² = a² - 2ab + b²
B. a(a - b) = a² - ab
C. a² - b² = (a - b)²
D. a² - b² = (a + b)(a - b)

答案： D

10. 新考向 古算题 (烟台中考)南宋数学家杨辉在其著作《详解九章算法》中揭示了(a + b)ⁿ(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将其称为“杨辉三角”.
(a + b)⁰ = 1                                                1
(a + b)¹ = a + b                                         1 1
(a + b)² = a² + 2ab + b²                           1 2 1
(a + b)³ = a³ + 3a²b + 3ab² + b³              1 3 3 1
(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴ 1 4 6 4 1
则(a + b)⁹展开式中所有项的系数和是( )
A. 128
B. 256
C. 512
D. 1024

答案： C [解析]由“杨辉三角”的规律可知，(a + b)⁹展开式中所有项的系数和为(1 + 1)⁹ = 2⁹ = 512。故选C。

11. (潍坊中考)若2ˣ = 3, 2ʸ = 5,则2ˣ⁺ʸ = ________.

答案： 15

12. 新考向 初高衔接 阅读理解：引入新数i,新数i满足分配律、结合律、交换律,已知i² = -1,那么(1 + i)(1 - i) = ________.

答案： 2

13. 新教材 变式题 将多项式x² + 4加上一个整式,使它成为一个完全平方式,试写出满足上述条件的三个整式：________, ________, ________.

答案： 4x， - 4x，$\frac{1}{16}$x⁴ [解析]设这个整式为Q，如果这里首末两项是x和2这两个数的平方，那么中间一项为加上或减去x和2积的2倍，故Q = ±4x；如果这里首末两项是Q和4，则乘积项是$x² = 2×2×\frac{1}{4}x²$，
∴$Q = (\frac{1}{4}x²)² = \frac{1}{16}x⁴$。故本题答案为$4x， - 4x，\frac{1}{16}x⁴$。

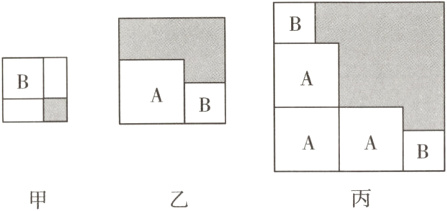
14. 辨思维 数形结合 (安徽期中)有边长为a的大正方形A和边长为b的小正方形B,现将B放在A内部得到图甲,将A, B并列放置后,构造新的正方形得到图乙,图甲和图乙阴影部分的面积分别是1和12.
(1)根据图甲、乙中的面积关系,可以得到a - b = ________, ab = ________.
(2)若3个正方形A和2个正方形B按图丙摆放,阴影部分的面积为________.

答案：
(1) 1；6
(2) 29 [解析]
(1)图甲中阴影部分面积可以表示为$(a - b)² = 1$，
∴a - b = 1。图乙中阴影部分面积可以表示为$(a + b)² - a² - b² = 2ab = 12$，
∴ab = 6。
(2)图丙中阴影部分面积为$(2a + b)² - 3a² - 2b² = 4a² + 4ab + b² - 3a² - 2b² = a² + 4ab - b² = (a + b)(a - b) + 4ab$。
∵a - b = 1，ab = 6，$(a + b)² = (a - b)² + 4ab$，
∴$(a + b)² = 1² + 4×6 = 25$，
∴a + b = 5（负值舍去），
∴(a + b)(a - b) + 4ab = 5×1 + 4×6 = 29。