第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1. 下列不等式是一元一次不等式的是( )
A. $3x - 2<4$
B. $x^{2}>42 - 3x$
C. $\frac{1}{x}<2$
D. $4x - 3<2y - 7$
A. $3x - 2<4$
B. $x^{2}>42 - 3x$
C. $\frac{1}{x}<2$
D. $4x - 3<2y - 7$
答案:
A
2. (杭州中考)若$a>b$,则( )
A. $a - 1\geqslant b$
B. $b + 1\geqslant a$
C. $a + 1>b - 1$
D. $a - 1>b + 1$
A. $a - 1\geqslant b$
B. $b + 1\geqslant a$
C. $a + 1>b - 1$
D. $a - 1>b + 1$
答案:
C
3. (河北中考)语句“$x$的$\frac{1}{8}$与$x$的和不超过5”可以表示为( )
A. $\frac{x}{8}+x\leqslant5$
B. $\frac{x}{8}+x\geqslant5$
C. $\frac{8}{x + 5}\leqslant5$
D. $\frac{x}{8}+x = 5$
A. $\frac{x}{8}+x\leqslant5$
B. $\frac{x}{8}+x\geqslant5$
C. $\frac{8}{x + 5}\leqslant5$
D. $\frac{x}{8}+x = 5$
答案:
A
4. 关于$x$的不等式$2x - a\leqslant1$的解集如图所示,则$a$的值是( )
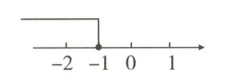
A. 0
B. -3
C. -2
D. -1

A. 0
B. -3
C. -2
D. -1
答案:
B
5. 新教材 变式题 四个小朋友玩跷跷板,他们的体重分别为$P$,$Q$,$R$,$S$,如图所示,则他们的体重大小关系是( )

A. $P>R>S>Q$
B. $Q>S>P>R$
C. $S>P>Q>R$
D. $S>P>R>Q$

A. $P>R>S>Q$
B. $Q>S>P>R$
C. $S>P>Q>R$
D. $S>P>R>Q$
答案:
D
6. (芜湖期中)解不等式$\frac{3 + x}{5}\leqslant\frac{2x + 4}{3}+2$时,去分母步骤正确的是( )
A. $3 + x\leqslant2x + 4 + 2$
B. $3 + x\leqslant2x + 4 + 30$
C. $3(3 + x)\leqslant5(2x + 4)+2$
D. $3(3 + x)\leqslant5(2x + 4)+30$
A. $3 + x\leqslant2x + 4 + 2$
B. $3 + x\leqslant2x + 4 + 30$
C. $3(3 + x)\leqslant5(2x + 4)+2$
D. $3(3 + x)\leqslant5(2x + 4)+30$
答案:
D
7. (赤峰中考)不等式组$\begin{cases}x + 1\geqslant2\\9 - x<2x\end{cases}$的解集在数轴上表示正确的是( )


答案:
C
8. 辨思维 易错题 (呼和浩特中考)若不等式$\frac{2x + 5}{3}-1\leqslant2 - x$的解集中$x$的每一个值,都能使关于$x$的不等式$3(x - 1)+5>5x + 2(m + x)$成立,则$m$的取值范围是( )
A. $m>-\frac{3}{5}$
B. $m<-\frac{1}{5}$
C. $m<-\frac{3}{5}$
D. $m>-\frac{1}{5}$
A. $m>-\frac{3}{5}$
B. $m<-\frac{1}{5}$
C. $m<-\frac{3}{5}$
D. $m>-\frac{1}{5}$
答案:
C
9. (镇江中考)下列各数轴上表示的$x$的取值范围可以是不等式组$\begin{cases}x + 2>a\\(2a - 1)x - 6<0\end{cases}$的解集的是( )


答案:
B
10. 新课标 模型观念 在一次“青年大学习”知识竞赛中,竞赛试题共有25道,每道题都给出了四个答案,其中只有一个答案是对的,要求学生把正确答案选出来,每道题选对得4分,不选或错选扣2分. 如果小明在本次竞赛中,得分不低于80分,那么他至少选对( )题.
A. 20道
B. 21道
C. 22道
D. 23道
A. 20道
B. 21道
C. 22道
D. 23道
答案:
C
11. 如果关于$x$的不等式$(a + 1)x>a + 1$的解集为$x<1$,那么$a$的取值范围是________.【变式训练→B卷T11】
答案:
a<-1
12. (温州中考)不等式组$\begin{cases}x - 3<0\\\frac{x + 4}{2}\geqslant1\end{cases}$的整数解的个数为________.
答案:
5
13. 辨思维 易错题 若关于$x$的不等式组$\begin{cases}2x>3x - 3\\3x - a>5\end{cases}$有实数解,则$a$的取值范围是________.
答案:
a<4
14. 新考向 开放题 (淮南期末)如图,某同学设计了一种计算流程图,据图完成下列问题.
(1)任意写出一个实数,使得该数经过一次运行就能输出结果,则该数可以为________.
(2)如果要使开始输入的$x$的值经过两次运行才能输出结果,那么$x$的整数值为________.

(1)任意写出一个实数,使得该数经过一次运行就能输出结果,则该数可以为________.
(2)如果要使开始输入的$x$的值经过两次运行才能输出结果,那么$x$的整数值为________.

答案:
(1)3(答案不唯一)
(2)1或2
(1)3(答案不唯一)
(2)1或2
15. (滁州期中)阅读下面的解题过程,再解题.
已知$a>b$,试比较$-2025a + 1$与$-2025b + 1$的大小.
解:$\because a>b$,①
$\therefore -2025a>-2025b$,②
$\therefore -2025a + 1>-2025b + 1$.③
问:(1)上述解题过程中,从第________步开始出现错误.
(2)请写出错误的原因.
(3)请写出正确的解题过程.
已知$a>b$,试比较$-2025a + 1$与$-2025b + 1$的大小.
解:$\because a>b$,①
$\therefore -2025a>-2025b$,②
$\therefore -2025a + 1>-2025b + 1$.③
问:(1)上述解题过程中,从第________步开始出现错误.
(2)请写出错误的原因.
(3)请写出正确的解题过程.
答案:
解:
(1)②
(2)不等式两边都乘同一个负数,不等号的方向没有改变. (合理即可)
(3)
∵$a>b$,
∴$-2025a<-2025b$,
∴$-2025a + 1<-2025b + 1$.
(1)②
(2)不等式两边都乘同一个负数,不等号的方向没有改变. (合理即可)
(3)
∵$a>b$,
∴$-2025a<-2025b$,
∴$-2025a + 1<-2025b + 1$.
16. 解不等式,并把解集在数轴上表示出来.
(1)(金华中考)$5x - 5<2(2 + x)$
(2)$\frac{x - 1}{3}+1\geqslant\frac{x + 1}{2}$
(1)(金华中考)$5x - 5<2(2 + x)$
(2)$\frac{x - 1}{3}+1\geqslant\frac{x + 1}{2}$
答案:
解:
(1)
∵$5x - 5<2(2 + x)$,
∴$5x - 5<4 + 2x$,
∴$3x<9$,
∴$x<3$. 在数轴上的表示如下:
−1 0 1 2 3
(2)去分母,得$2(x - 1)+6\geq3(x + 1)$. 去括号,得$2x - 2 + 6\geq3x + 3$. 移项、合并同类项,得$-x\geq-1$. 系数化为1,得$x\leq1$. 在数轴上的表示如
★易错警示
解一元一次不等式的“四点注意”
(1)去分母:去分母时要注意每一项都要乘分母的最小公倍数. 不要漏乘不含分母的项.
(2)去括号:根据乘法的分配律不要漏乘项.
(3)移项:移项要注意改变该项的符号,不等号方向不变.
(4)系数化为1:两边都除以负数时注意不等号方向要改变.
(1)
∵$5x - 5<2(2 + x)$,
∴$5x - 5<4 + 2x$,
∴$3x<9$,
∴$x<3$. 在数轴上的表示如下:
−1 0 1 2 3
(2)去分母,得$2(x - 1)+6\geq3(x + 1)$. 去括号,得$2x - 2 + 6\geq3x + 3$. 移项、合并同类项,得$-x\geq-1$. 系数化为1,得$x\leq1$. 在数轴上的表示如
★易错警示
解一元一次不等式的“四点注意”
(1)去分母:去分母时要注意每一项都要乘分母的最小公倍数. 不要漏乘不含分母的项.
(2)去括号:根据乘法的分配律不要漏乘项.
(3)移项:移项要注意改变该项的符号,不等号方向不变.
(4)系数化为1:两边都除以负数时注意不等号方向要改变.
17. 解不等式组.
(1)$\begin{cases}3x - 2<4 ①\\2(x - 1)\leqslant3x + 1 ②\end{cases}$
(2)(常德中考)$\begin{cases}2x - 1<x + 4 ①\\\frac{2}{3}x-\frac{3x + 1}{2}\leqslant\frac{1}{3} ②\end{cases}$
(1)$\begin{cases}3x - 2<4 ①\\2(x - 1)\leqslant3x + 1 ②\end{cases}$
(2)(常德中考)$\begin{cases}2x - 1<x + 4 ①\\\frac{2}{3}x-\frac{3x + 1}{2}\leqslant\frac{1}{3} ②\end{cases}$
答案:
解:
(1)解不等式①,得$x<2$;解不等式②,得$x\geq-3$,
∴原不等式组的解集是$-3\leq x<2$.
(2)解不等式①,得$x<5$;解不等式②,得$x\geq-1$,
∴原不等式组的解集为$-1\leq x<5$.
(1)解不等式①,得$x<2$;解不等式②,得$x\geq-3$,
∴原不等式组的解集是$-3\leq x<2$.
(2)解不等式①,得$x<5$;解不等式②,得$x\geq-1$,
∴原不等式组的解集为$-1\leq x<5$.
18. 已知$x = 3$是关于$x$的不等式$3x-\frac{ax + 2}{2}>\frac{2x}{3}$的一个解,求$a$的取值范围.
答案:
解:将$x = 3$代入不等式,得$9-\frac{3a + 2}{2}>2$,解这个不等式,得$a<4$,
∴$a$的取值范围为$a<4$.
∴$a$的取值范围为$a<4$.
19. 新教材 变式题 已知方程组$\begin{cases}x + y=-a - 7\\x - y=1 + 3a\end{cases}$的解$x$为非正数,$y$为负数.
(1)求$a$的取值范围.
(2)化简:$\vert a - 6\vert+\vert a + 3\vert$.
(1)求$a$的取值范围.
(2)化简:$\vert a - 6\vert+\vert a + 3\vert$.
答案:
解:
(1)$\begin{cases}x + y=-a - 7&①\\x - y=1 + 3a&②\end{cases}$,① + ②,得$2x = 2a - 6$,解得$x = a - 3$;① - ②,得$2y=-4a - 8$,解得$y=-2a - 4$.
∵$x$为非正数,$y$为负数,
∴$\begin{cases}a - 3\leq0\\-2a - 4<0\end{cases}$,解得$-2<a\leq3$.
(2)
∵$-2<a\leq3$,
∴$a - 6<0$,$a + 3>0$,故$\vert a - 6\vert+\vert a + 3\vert=6 - a + a + 3 = 9$.
(1)$\begin{cases}x + y=-a - 7&①\\x - y=1 + 3a&②\end{cases}$,① + ②,得$2x = 2a - 6$,解得$x = a - 3$;① - ②,得$2y=-4a - 8$,解得$y=-2a - 4$.
∵$x$为非正数,$y$为负数,
∴$\begin{cases}a - 3\leq0\\-2a - 4<0\end{cases}$,解得$-2<a\leq3$.
(2)
∵$-2<a\leq3$,
∴$a - 6<0$,$a + 3>0$,故$\vert a - 6\vert+\vert a + 3\vert=6 - a + a + 3 = 9$.
20. 新考向 新定义 (合肥期中)定义新运算“$\oplus$”如下:当$m\geqslant n$时,$m\oplus n=mn + n$;当$m<n$时,$m\oplus n=mn - n$.
(1)求$-\sqrt{2}\oplus(-1)$的值.
(2)若$4\oplus(x + 3)>0$,求$x$的取值范围.
(1)求$-\sqrt{2}\oplus(-1)$的值.
(2)若$4\oplus(x + 3)>0$,求$x$的取值范围.
答案:
解:
(1)
∵$-\sqrt{2}<-1$,
∴$-\sqrt{2}\oplus(-1)=(-\sqrt{2})×(-1)-(-1)=\sqrt{2}+1$.
(2)
∵$4\oplus(x + 3)>0$,
∴当$4\geq x + 3$,即$x\leq1$时,$4(x + 3)+(x + 3)>0$,解得$x>-3$,
∴$x$的取值范围为$-3<x\leq1$;当$4<x + 3$,即$x>1$时,$4(x + 3)-(x + 3)>0$,解得$x>-3$,
∴$x$的取值范围是$x>1$. 综上所述,$x$的取值范围是$x>-3$.
(1)
∵$-\sqrt{2}<-1$,
∴$-\sqrt{2}\oplus(-1)=(-\sqrt{2})×(-1)-(-1)=\sqrt{2}+1$.
(2)
∵$4\oplus(x + 3)>0$,
∴当$4\geq x + 3$,即$x\leq1$时,$4(x + 3)+(x + 3)>0$,解得$x>-3$,
∴$x$的取值范围为$-3<x\leq1$;当$4<x + 3$,即$x>1$时,$4(x + 3)-(x + 3)>0$,解得$x>-3$,
∴$x$的取值范围是$x>1$. 综上所述,$x$的取值范围是$x>-3$.
六、(本题满分12分)
21. 辨思维 易错题 试确定实数$a$的取值范围,使不等式组$\begin{cases}\frac{x}{2}+\frac{x + 1}{3}>0\\x+\frac{5a + 4}{3}>\frac{4}{3}(x + 1)+a\end{cases}$恰好有2个整数解.
21. 辨思维 易错题 试确定实数$a$的取值范围,使不等式组$\begin{cases}\frac{x}{2}+\frac{x + 1}{3}>0\\x+\frac{5a + 4}{3}>\frac{4}{3}(x + 1)+a\end{cases}$恰好有2个整数解.
答案:
解:$\begin{cases}\frac{x}{2}+\frac{x + 1}{3}>0&①\\x+\frac{5a + 4}{3}>\frac{4}{3}(x + 1)+a&②\end{cases}$,解不等式①,得$x>-\frac{2}{5}$;解不等式②,得$x<2a$,
∴原不等式组的解集为$-\frac{2}{5}<x<2a$. 又
∵原不等式组恰好有2个整数解,
∴$x = 0$,$1$,
∴$1<2a\leq2$,
∴$\frac{1}{2}<a\leq1$.
∴原不等式组的解集为$-\frac{2}{5}<x<2a$. 又
∵原不等式组恰好有2个整数解,
∴$x = 0$,$1$,
∴$1<2a\leq2$,
∴$\frac{1}{2}<a\leq1$.
七、(本题满分12分)
22. (哈尔滨中考)昌云中学计划为地理兴趣小组购买大、小两种地球仪,购买1个大地球仪和3个小地球仪需用136元;购买2个大地球仪和1个小地球仪需用132元.
(1)求每个大地球仪和每个小地球仪各多少元.
(2)昌云中学决定购买以上两种地球仪共30个,总费用不超过960元,那么昌云中学最多可以购买多少个大地球仪?
22. (哈尔滨中考)昌云中学计划为地理兴趣小组购买大、小两种地球仪,购买1个大地球仪和3个小地球仪需用136元;购买2个大地球仪和1个小地球仪需用132元.
(1)求每个大地球仪和每个小地球仪各多少元.
(2)昌云中学决定购买以上两种地球仪共30个,总费用不超过960元,那么昌云中学最多可以购买多少个大地球仪?
答案:
解:
(1)设每个大地球仪$x$元,每个小地球仪$y$元. 根据题意可得$\begin{cases}x + 3y=136\\2x + y=132\end{cases}$,解得$\begin{cases}x = 52\\y = 28\end{cases}$. 答:每个大地球仪52元,每个小地球仪28元.
(2)设购买大地球仪$a$个,则购买小地球仪$(30 - a)$个. 根据题意可得$52a + 28(30 - a)\leq960$,解得$a\leq5$. 答:昌云中学最多可以购买5个大地球仪.
(1)设每个大地球仪$x$元,每个小地球仪$y$元. 根据题意可得$\begin{cases}x + 3y=136\\2x + y=132\end{cases}$,解得$\begin{cases}x = 52\\y = 28\end{cases}$. 答:每个大地球仪52元,每个小地球仪28元.
(2)设购买大地球仪$a$个,则购买小地球仪$(30 - a)$个. 根据题意可得$52a + 28(30 - a)\leq960$,解得$a\leq5$. 答:昌云中学最多可以购买5个大地球仪.
八、(本题满分14分)
23. 新课标 模型观念 (淮北期中)陈老师的家乡出产青李,因雪峰山特殊的地形形成特殊的气候,所以青李的品质很高. 家乡人成立了雪峰商会,其中有一专项就是青李的销售. 去年青李成熟之际,商会收集了大量的青李,用A,B两种型号的货车分两批装箱运往C市销售,具体运输情况如下表(备注:第一批、第二批每辆货车均满载):
|批次|第一批|第二批|
|----|----|----|
|A种型号货车的数量/辆|8|15|
|B种型号货车的数量/辆|4|10|
|累计运输青李的质量/吨|44|95|
(1)求A,B两种型号货车每辆满载分别能运多少吨青李.
(2)已知A种型号货车满载运往C市一趟的运费为540元,B种型号货车满载运往C市一趟的运费为740元,商会后续又筹集了40吨青李,现需要10辆货车运送青李. 为控制运费不超过6600元,试问有哪几种方案可以一次性将这批青李运往目的地?
23. 新课标 模型观念 (淮北期中)陈老师的家乡出产青李,因雪峰山特殊的地形形成特殊的气候,所以青李的品质很高. 家乡人成立了雪峰商会,其中有一专项就是青李的销售. 去年青李成熟之际,商会收集了大量的青李,用A,B两种型号的货车分两批装箱运往C市销售,具体运输情况如下表(备注:第一批、第二批每辆货车均满载):
|批次|第一批|第二批|
|----|----|----|
|A种型号货车的数量/辆|8|15|
|B种型号货车的数量/辆|4|10|
|累计运输青李的质量/吨|44|95|
(1)求A,B两种型号货车每辆满载分别能运多少吨青李.
(2)已知A种型号货车满载运往C市一趟的运费为540元,B种型号货车满载运往C市一趟的运费为740元,商会后续又筹集了40吨青李,现需要10辆货车运送青李. 为控制运费不超过6600元,试问有哪几种方案可以一次性将这批青李运往目的地?
答案:
解:
(1)设A种型号货车每辆满载能运$x$吨青李,B种型号货车每辆满载能运$y$吨青李. 依题意,得$\begin{cases}8x + 4y=44\\15x + 10y=95\end{cases}$,解得$\begin{cases}x = 3\\y = 5\end{cases}$. 答:A种型号货车每辆满载能运3吨青李,B种型号货车每辆满载能运5吨青李.
(2)设需$m$辆A种型号货车,$(10 - m)$辆B种型号货车可以一次性将这批青李运往目的地. 依题意,得$\begin{cases}3m + 5(10 - m)\geq40\\540m + 740(10 - m)\leq6600\end{cases}$,解得$4\leq m\leq5$. 又
∵$m$为正整数,
∴$m = 4$或5,
∴运输方案有两种:①4辆A种型号货车,6辆B种型号货车;②5辆A种型号货车,5辆B种型号货车.
(1)设A种型号货车每辆满载能运$x$吨青李,B种型号货车每辆满载能运$y$吨青李. 依题意,得$\begin{cases}8x + 4y=44\\15x + 10y=95\end{cases}$,解得$\begin{cases}x = 3\\y = 5\end{cases}$. 答:A种型号货车每辆满载能运3吨青李,B种型号货车每辆满载能运5吨青李.
(2)设需$m$辆A种型号货车,$(10 - m)$辆B种型号货车可以一次性将这批青李运往目的地. 依题意,得$\begin{cases}3m + 5(10 - m)\geq40\\540m + 740(10 - m)\leq6600\end{cases}$,解得$4\leq m\leq5$. 又
∵$m$为正整数,
∴$m = 4$或5,
∴运输方案有两种:①4辆A种型号货车,6辆B种型号货车;②5辆A种型号货车,5辆B种型号货车.
查看更多完整答案,请扫码查看


